Nejste přihlášen/a.
Zdravím,
potřebovala bych pomoct s vyřešením 3 příkladů. Zkoušela jsem už všechno možné, co se normálně v goniometrii používá, ale výsledek pořád nevychází správně.
a) Určete, pro jaká x má daná rovnost smysl, a dokažte její správnost:
(1 tgx/1-tgx) = cos2x/(1-sin2x)
b) Řešte rovnice s neznámou x:
sin5x - sinx = cos3x
(1/(cosx*cosx)) √3 tgx = 1
Děkuji za snahu ![]()
0x
Zde je již jednou stejná otázka is návodem, jak řešit. Vidím, že zadání prvního příkladu jste opravila.
No, ono tady nejde o to, že bych nevěděla, jak bych na to měla jít, ale když to upravuji podle pravidel jako všechny ostatní příklady, tak mi to prostě nevychází. Třeba u toho a) mi vyjde správně jedna strana, ale u té druhé nevím, jak se k tomu dostat, prostě to nevychází, ať dělám, co dělám.
Levou upravíme tak, že tg(x) vyjádříme jako podíl sin(x)/cos(x):
Pravou stranu upravíme podle vzorců: sin 2x = 2 sin x cos x ; cos 2x = cos2 x - sin2 x ; sin2 x + cos2 x = 1
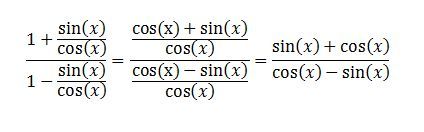
Děkuji ![]()
A nevíte náhodou, co udělat s těmi dalšími příklady? U prvního mi vychází rozklad na celý papír (bezvýsledně) a u druhého opakovaně záporný diskriminant...
sin5x - sinx = cos3x
(1/(cosx*cosx)) √3 tgx = 1
Nezní ten poslední příklad takto:
1/(cos(x)*cos(x)) + √3 tg(x) = 1
Alespoň v té minulé otázce to tak je, to znamená, že před √3 má být plus.
sin5x - sinx = cos3x... zde bych použil vzorec sinα - sinβ = 2cos[[α+β] /2] * sin[[α-β]/2]
Levou stranu upravíme:
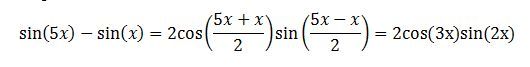
Dostaneme rovnici 2cos(3x)sin(2x) = cos(3x).
Výraz na pravé straně převedeme na levou stranu: 2cos(3x)sin(2x) - cos(3x) = 0.
Vytkneme cos(3x) : cos(3x)⋅[2sin(2x) _ 1] = 0.
Součin bude roven nule, když alespoň jeden činitel bude roven nule. Takže nyní stačí vyřešit tyto dvě rovnice:
cos(3x) = 0 nebo 2sin(2x) _ 1 = 0, čili sin(2x) = ½
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.