Ahoj, kamarádka je v prváku na střední a potřebovala by pomoct s tímto příkladem. Je třeba spočítat síly, vyšlo jí F1=250N, F2=433N. Podle jejího učitele by to ale mělo vyjít F2=20*√2, což mi ale přijde jako kravina. Může někdo prosím poradit? ![]()
Omlouvám se, prý by mělo vyjít 20*√3, ale přijde mi to pořád jako hloupost ![]()
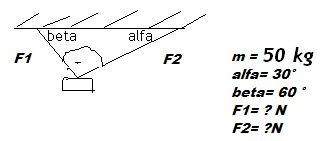
1x
závaží má být přesně vlevo vzdálené v 1/4 od místa zavěšení.Vychází se z vlastností trojúhelníka a goniometrických funkcí. Vzdálenost závěsů si klidně zvol 1m. Svislé síly mi pak vycházejí Fvlevo(svislá) 37,5kg (50x0,75) a vlevo Fvpravo(svislá) 12,5kg (50x0,25). Dohromady 50kg. Z toho se pak dají odvodit šikmé působící síly,kdy svislou sílu Fx převedeš přes sínus či kosínus na šikmou. F vpravo šikmá = F vpravo svislá / (lomeno) sinus 30. Tedy Fvpravo šikmá = 12,5/0.5 = 25kg.F vlevo šikmá je 37,5 /sin 60 = 43,303kg. Na Newtony si to už převeď sám.
doplněno 25.09.12 20:14:jinývýsledek jsem nenalezl. . . .
1x
Miramira se na problém dívá jako na ve dvou bodech podepřený nosník se zatížením v jedné čtvrtině mezi podpěrami. Proč ne, dochází ke správnému výsledku, ale lze poiužít i přímo prostý rozklad svislé síly F ∼ 50 kg (tedy F = 500 N _ přibližně) do dvou kolmých směrů, čímž dostaneme kontrolní výsledek F1 = F . cos α = ½ 500 N, F2 = F.cos β = 250 .√3., ve shodě s výše uvedenými výsledku. Výsledek pana učitele trochu připomíná ten 250 .√3, ale liší se od něj na první pohled řádově, což by mohlo být tím, že počítá v kilogramech (přesněji v kilopondech, neb kilogram není síla, leč hmotnost), ale stejně není jasný ten číselná rozdíl mezi 20 a 25 (ono, pravda 25 kg odpovídá přesněji 245 N, alejednak je to výrazně menší nepřesnost, a jednak, pokud bypan učitel nepoužíval Newtony, tak by vůbec nebyl důvod takovouto korekci uvažovat. Prostě nevím. Ještě mne napadllo, že panu učiteli přo opisování ta pštka mezi 2 a 0 vypadla a že měl skutečně na mysli 250 .√3.
0x
příklad je na rovnováhu dvou vektorů. Horizontální složky se ruší, součet vertikálních je 50, vychází dvě rovnice o dvou neznámých.
Dopočítejte to někdo, protože mě se do toho nechce. ![]()
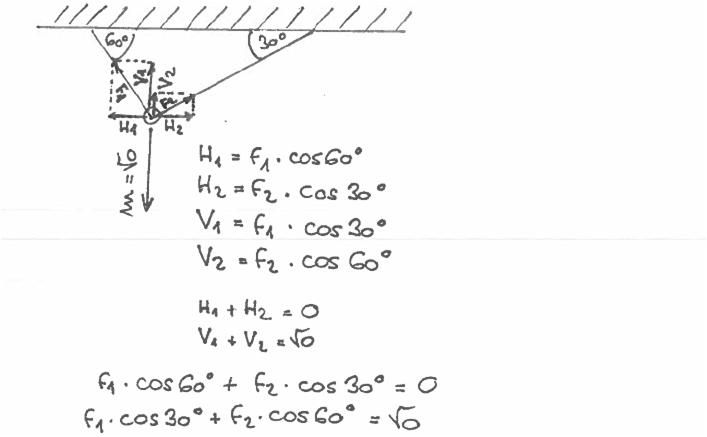
Malá připomínka, složky H1 a H2 jsou opačné oriantace, takže ta první rovnice bude H1 - H2 = 0. Pak už ty dvě rovnice snadno vyřeším, ale řekl bych, že je to zbytečná komplikace. Leda z didaktických důvodů; správně to samozřejmě je (tedy až na to znaménko).
doplněno 26.09.12 19:27:(Vypočteme to tak, že první rovnici (samozřejmě s tím mínusem)
znásobíme cos 60°, tu druhou cos 30° a sečteme. (A samozřejmě na závěr vše převedeme na vhodné jednotky.¨![]()
všiml jsem si že jste znalec a mistr pedagogiky. Jenže tady nejde o úhly na trojúhelníku, ale o počítání s vektory a vektorovou rovnováhu sil.
H1+H2=0 a nikdy jinak. Zkuste uhodnout proč.
Prosím vás, taky umím vektorovou analýzu, a myslím že lépe, než vy. Možná bychom měli začít tím, že si vyjasníme pojmy. Tak, jak H1 a H2 dosazujete do rovnic, jsou to čísla a ne vektory; co je to za čísla? Velikosti? Souřadnice? A jen na okraj: když vyřeším vaše rovnice, vyjde mi F1 = 50 √3, F2 = _25. Popřemýšlejte o tom.
doplněno 27.09.12 12:00:A ta poznámka o mistru pedagogiky, to je váš mindrák a váš problém.
chacha![]()
![]()
![]() . Vidím že jste lehce nedotčený disiplínou zvanou mechanika nebo jste tehdá ve škole chyběl? To co nahoře vidíte, je základní úloha na rovnováhu vektorů.
. Vidím že jste lehce nedotčený disiplínou zvanou mechanika nebo jste tehdá ve škole chyběl? To co nahoře vidíte, je základní úloha na rovnováhu vektorů.
Jak vám může vyjít F1 v plusu a F2 v minusu? Myslíte, že jeden prut táhne a druhý tlačí? No tak to možná někde na základní škole, ale v praxi asi ne. Kdybyste něco takového řekl u zkoušky, pak už byste nemusel mluvit dál.
A taky přidám doplněk. Já jsem z učitelské rodiny. Mě z klidu nevyvedete.
Prosím vás, přečtěte si, na co odpovídáte. Ta opačná znaménka vyjdouy VÁM, z těch vašich rovnic, tak kdo by vyletěl od zkoušky? Právě proto musí být ta první rovnice s mínusem.
doplněno 28.09.12 12:21:A co kdybyste se zamyslel nad mým návrhem, ujasnit si pojmy? Kdybyste napsal, co je co, možná bychom se dohodli. Souhlasím s tím, že vektory H1, H2, které jste namaloval, se po sečtení oanulují, aler vy ve svých výpočtech počítáte s čísly H1, H2. Kdybyste napsal, co ta čísla pro vás znamenají, možná byste nekecal pitomosti. Tak, jak jste to namaloval vy, četl bych to tak, že f1,f2 jsou velikosti vektorů F1,F2, které jste tam namaloval, a H1,H2 jsou velikosti vektorů H1,H2,; tak to odpovídá vašemu výpočtu, a protože ty vektory jsou (s tím souhlasím) opačně orientované, tak při jejich sčítání se velikosti musí odečíst. Kdybyste měl na mysli, že H1, H2 jsou souřadnice těch vektorů, (souřadná soustava by patrně byla standardně orientovaná), pak ano, pak by se sčítaly, ale to byste je musel spočítat správně,
doplněno 28.09.12 12:39:Trochu se obávám, že jsem se nechal poněkud unést. Píši Vám do vnitřní pošty, snad si to vyjasníme.
doplněno 29.09.12 15:19:jen poznámka, navrhuji vést věcnou diiskuzi bez invektiv.
0x
Kolega Figurek zřejmě nemá zájem o věcnou diskuzi, takže sem napíšu své řešení, a to co nejúplněji, abych předešel případné nedorozumění; kolega Figurek si to může přečíst anebo ne, to je na něm.
Tak především vyjdu z jeho obrázku, který mi přijde pěkný, ale vyjasním nejprve pojmy. Na obrázku vidím několik vektorů a dále budu počítat s čísly, takže: vektory budu značit tučně podtrženě, a budu je chápat tak, jak je kolega Figurek namaloval, s orientací danou směrem šipky. Takže v obrázku vidím vektor m odbovídající zatížení , směr tohoto vektoru je ve směru gravitace, velikost | m | = m = 50 (kilopondů), Dále pak vektory F1 a F2, jejichž velikosti budou F1 a F2. Podmínka rovnováhy je nyní, že součet těchto VEKTORŮ je nulový, tedy
m + F1 + F2= 0
(na pravé straně není nula jako číslo, ale nulový vektor). To je ovšem rovnice vektorová tak to zřejmě myslel i kolega Figurek, v tom se shodneme.
tuto rovnici lze řešit buď pomocí vhodného souřadného systému, ( k tomu se vrátím), nebo rozkladem na složky, což jsou opět vektory. Zde jde o vektory H1, H2, V1, V2 a jejich velikosti H1, H2, V1, V2 (aspoň tak je budu chápat já, nemohu mluvit za kolegu Figurka, který se k tomuto tématu nevyjádřil) Velikosti budou kladná čísla a lze souhlasit s tím, jak ty vektory kolega na obrázku orientoval, tedy dejme tomu vektor H1 bude vektor velikosti H1>0, orientovaný "zprava doleva", vektor H2 bude ležet t téže přímce, ale bude orientovaný "zleva doprava", tedy opačně, atd. Takže rovnice rovnováhy, zapsané ve složkách budou
H1 + H2 = 0, V1 + V2 + m = 0
Jak je teď zapíšeme v číslech?
Velikosti H1, H2, V1 V2 jsou následovné:
H1 = F1 cos 60°, H2 = F2 cos 30°
V1 = F1 cos 30°, V2 = F2 cos 60°
(použil jsem vzorečky kolegy Figurka, které chápu jako výpočet velikostí; v tomto směru jsem je kontroloval a souhlasím. Jak je chápe kolega Figurek, nevím, protože se o tom odmítl bavit. Původně jsem myslel, že je chápe také tak, ale nemohu mluvit za něj.)
Takže jak teď sečteme složky? Nikoli samozřejmě tak, že napíšeme H1 + H2 = 0, V1 + V2 + m = 0, Vektory v jedné přímce se sčítají tak, že velikosti vektorů stejně orientovaných se sečtou, velikosti opačně orientovaných vektorů se odečtou. Tedy z druhé rovnice dostaneme
F1 cos 30°+ F2 cos 60° _ 50 = 0, odkud plyne
F1 cos 30°+ F2 cos 60° = 50
a z první rovnice dostaneme
F1 cos 60° _ F2 cos 30° = 0
. Řešení těchto dvou rovnic pak je
F1 = 50 √3, F2 = 25
ve shodě s tím, co vyšlo tazateli a následné různými postupy spočedl Miramira a já.
(Naproti tomu rovnice
F1 cos 30°+ F2 cos 60° = 50F1 cos 60° + F2 cos 30° = 0
mají řešení F1 = 50 √3, F2 = _25, které je poněkud podivné. Ostatně, proč vlastně kolega Figurek tak bazíruje na těchto rovnicích a n na rovnicích
F1 cos 30°+ F2 cos 60° = _50
F1 cos 60° + F2 cos 30° = 0? )
Slíbil jsem ještě řešení přes souřadný systém, ale to je další téma a přidám ho do doplňku.
doplněno 30.09.12 19:34:
5ešení pomocí souřadníc:¨Zavedu kartézské souřadnice, bejlépe tak, že počátek bude v bodě zavěšení břemene, osa x bude vodorovná a kladně orientovaná (jak je v kraji zvykem) zleva doprava, osa y bude svislá, s kladným směrem "vzhůru". Pak bude vhodné, aby čísla H1, H2, V1 atd. mela význam souřadnic a ne velikostí; číselná hodnota (tedy absolutní hodnota) se nezmění, ale změní se eventuálně znaménko, Speciálně m bude záporné a stejně tak H1. Pak bude zápis
H1 + H2 = 0, V1 + V2 + m = 0
v pořádku, ovšem s tím, že m = -50, H1 = _F1 cos 60 °.
(Nebo, chcete-li, H1 = + F1 cos 120°, což je ve výsledku totéž.)
Takže "mezirovnice"se trochu změnily, ale nakonec dojdeme opět k rovnicím
F1 cos 30°+ F2 cos 60° = 50F1 cos 60° _ F2 cos 30° = 0
qoud erat demonstrandum.
Na závěr ke kolegovi Figurkovi: Jak jsem říjkal, zda si to přečte nebo ne, je na něm, ale myslím, že by prokázal smysl pro gentlemanské chování, kdyby si to přečetl a buď uznal, že mám pravdu, nebo mi věcně ukázal, v čem konkrétně se mýlím.
doplněno 01.10.12 08:50:
Opravuji: myslím, že případná Figurkova odpověd není jen projev gentlemanství, ale, zvlášť po jeho hulvátské odpovědi, věc elementární sluušnosti. Ale po pravdě, právě vzhledem k jeho hulvátství, v to moc nedoufám.
doplněno 02.10.12 08:33:Jak jsem tušil, Figurek se neozval. Zřejmě není schopen slušného chování a asi ani nechápe ppodstatu problému; pro úplnost odkazuji na otázku, kterou založil a která pravděpodobně s tímto souvisí:
doplněno 20.10.12 13:37:Že se ještě k toéto otázce vracím: v diskusi s Figurkem jsme občas používali řekněme ostřejší formulace, které možná byly pochopitelné, možná ne, ale rozhodně neměly co dělat s faktickou podstatou věci. V soukromém mailo ve vnitřní poště jsem se mu za své formulace, které se ho mohly dotknout, omluvil a požádal o prominutí, a naopak ze své strany rovněž vše promíjím. Jelikož ale mnohé invektivy padly zde veřejně, pokládám za správné tuto omluvu zde veřejně uvést.
(Podstatu problému z hlediska faktického ponechávám na posouzení laskavých čtenářů.)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.