Trojúhelník - důkaz

Od: julkx 12.11.23 20:59 odpovědí: 12 změna: 13.11.23 02:21

Dobrý den, potřebovala bych pomoct s touto úlohou, vůbec ji nechápu a nevím jak na ní tak doufám, že se najde nějaká hodná duše a pomůže mi...

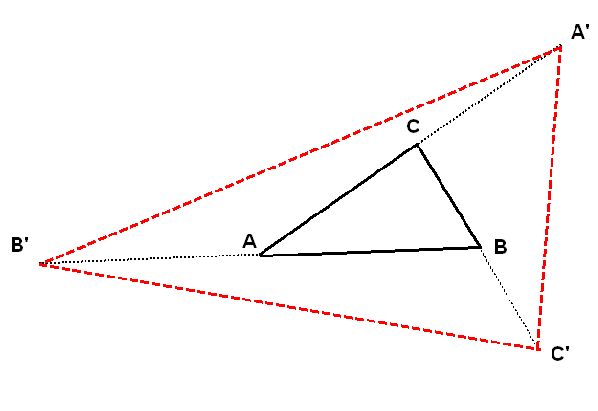
Trojúhelník ABC je pravoúhlý s pravým úhlem při vrcholu C. Body A′, B′, C′ jsou obrazy bodů A, B, C postupně ve středových souměrnostech se středy C, A, B. Dokažte, že platí

|AB|² +|BC|² +|CA|² =14·|AB|²

^{Doufám, že někdo pomůže, předem děkuji}

Odpovědět na otázku Skočit na nejnovější odpověď

12 odpovědí na otázku

Řazeno dle hodnocení

kdosi

12.11.23 21:02

[?]

Blbě jsi to opsalo, takhle to neplatí

julkxx

12.11.23 21:06

[?]

Pardon melo to byt |A’B’|na druhou + |B’C’| na druhou + |C’A’| na druhou = 14 . |AB| na druhou

[přidat komentář]

lmgify

12.11.23 23:19

[?]

Výpočet délky |AC|² z trojúhelníku ACC Pythagorovou větou:

|AC|² = |AC|² + |CC|² = |AC|² + (2.|BC|)² = |AC|² + 4.|BC|²

-------------------------------------------------------------------------------------------

Výpočet délky |AB|² z trojúhelníku BAA kosinovou větou:

|AB|² = |BA|² + |AA|² - 2.|BA|.|AA|.cos(BAA)

cos(BAA) = -cos(BAC) = -|AC|/|AB|

|AB|² = |AB|² + (2.|AC|²) + 2.|AB|.(2.|AC|).|AC|/|AB|

|AB|² = |AB|² + 4.|AC|² + 4.|AC|²

|AB|² = |AB|² + 8.|AC|²

-------------------------------------------------------------------------------------------

Výpočet délky |BC|² z trojúhelníku BBC kosinovou větou:

|BC|² = |BB|² + |BC|² - 2.|BB|.|BC|.cos(BBC)

cos(BBC) = -cos(CBA) = -|BC|/|AB|

|BC|² = (2.|AB|)² + |BC|² + 2.(2.|AB|).|BC|.|BC|/|AB|

|BC|² = 4.|AB|² + |BC|² + 4|BC|²

|BC|² = 4.|AB|² + 5.|BC|²

-------------------------------------------------------------------------------------------

|AB|² + |BC|² + |AC|² = |AB|² + 8.|AC|² + 4.|AB|² + 5.|BC|² + |AC|² + 4.|BC|² =

= 5.|AB|² + 9.|BC|² + 9.|AC|² =

= 5.|AB|² + 9.(|BC|² + |AC|²) =

= 5.|AB|² + 9.|AB|² =

= 14.|AB|²

julkx

12.11.23 23:22

[?]

Moc dekuji, ale moc se omlouvam ale kosinovou vetu jsme se jeste neucili… nevedel by jste prosim nejaky jiny zpusob? moc se omlouvam ze otracvuji ale i tak moc dekuji za toto vysvetleni

lmgify

12.11.23 23:26

[?]

Sežralo mi to ta očárkovaná písmenka, příspěvek přikládám jako textový soubor.

Pyth_soum.txt

1.21 kB

lmgify

12.11.23 23:29

[?]

Aha, tak teď to zase ztratilo ty druhé mocniny Ještě s tím budu bojovat a podívám se na tu náhradu kosinové věty.

julkx

12.11.23 23:32

[?]

děkuji jste opravdu zachrana

lmgify

13.11.23 02:04

[?]

Koukám na to už několik hodin a jednodušší řešení mě nenapadá.

Jsou to 3 nezávislé středové souměrnosti v sobě, takže vlastností středového zobrazení na podobnosti nejde využít. Je tam jen jeden pravý úhel, takže s tím taky nejde moc dělat. Je to celé vyosené, takže využití obloukových úhlů jsem také nenašel. Navíc se to ptá na součet všech čtverců stran, tedy je nutno ty strany znát nebo nějak dokázat faktor zvětšení, přičemž ten trojúhelník je převrácený naruby ... Prostě mě napadají jen krkolomná, strašně zdlouhavá řešení, za pomoci goniometrických funkcí.

Asi budeme muset počkat, s čím přijdou chytřejší přispěvatelé (@kartaginec?) nebo se budeš muset obrátit na forum.matweb.cz.

Co teď berete ve škole za látku? Třeba by to mohla být nápověda jakým směrem se ubírat k řešení.

lmgify

13.11.23 02:21

[?]

Jestli se náhodou dozvíš správné řešení ve škole dříve, než ti tady někdo poradí, můžeš nám ho sem přijít prozradit? Díky předem.

Skočit na otázku
Vložit novou otázku

[přidat komentář]

lmgify

12.11.23 23:23

[?]

Výpočet délky |AC|2 z trojúhelníku ACC Pythagorovou větou:

|AC|2 = |AC|2 + |CC|2 = |AC|2 + (2.|BC|)2 = |AC|2 + 4.|BC|2

-------------------------------------------------------------------------------------------

Výpočet délky |AB|2 z trojúhelníku BAA kosinovou větou:

|AB|2 = |BA|2 + |AA|2 - 2.|BA|.|AA|.cos(BAA)

cos(BAA) = -cos(BAC) = -|AC|/|AB|

|AB|2 = |AB|2 + (2.|AC|2) + 2.|AB|.(2.|AC|).|AC|/|AB|

|AB|2 = |AB|2 + 4.|AC|2 + 4.|AC|2

|AB|2 = |AB|2 + 8.|AC|2

-------------------------------------------------------------------------------------------

Výpočet délky |BC|2 z trojúhelníku BBC kosinovou větou:

|BC|2 = |BB|2 + |BC|2 - 2.|BB|.|BC|.cos(BBC)

cos(BBC) = -cos(CBA) = -|BC|/|AB|

|BC|2 = (2.|AB|)2 + |BC|2 + 2.(2.|AB|).|BC|.|BC|/|AB|

|BC|2 = 4.|AB|2 + |BC|2 + 4|BC|2

|BC|2 = 4.|AB|2 + 5.|BC|2

-------------------------------------------------------------------------------------------

|AB|2 + |BC|2 + |AC|2 = |AB|2 + 8.|AC|2 + 4.|AB|2 + 5.|BC|2 + |AC|2 + 4.|BC|2 =

= 5.|AB|2 + 9.|BC|2 + 9.|AC|2 =

= 5.|AB|2 + 9.(|BC|2 + |AC|2) =

= 5.|AB|2 + 9.|AB|2 =

= 14.|AB|2

liska5

13.11.23 00:20

[?]

Ještě češtinu: ..Nevěděl byste? To bys měl znát. My bychom to ocenili.

[přidat komentář]

lmgify

13.11.23 02:15

[?]

Zkusím sem ještě jednou vložit to původní řešení a nahradit všechny uvozovky za jiné.

==========================

Výpočet délky |A′C′|² z trojúhelníku A′CC′ Pythagorovou větou:

|A′C′|² = |A′C|² + |CC′|² = |AC|² + (2.|BC|)² = |AC|² + 4.|BC|²

-------------------------------------------------------------------------------------------

Výpočet délky |A′B′|² z trojúhelníku B′AA′ kosinovou větou:

|A′B′|² = |B′A|² + |AA′|² - 2.|B′A|.|AA′|.cos( B′AA′ )

cos( B′AA′ ) = -cos( BAC ) = -|AC|/|AB|

|A′B′|² = |AB|² + (2.|AC|²) + 2.|AB|.(2.|AC|).|AC|/|AB|

|A′B′|² = |AB|² + 4.|AC|² + 4.|AC|²

|A′B′|² = |AB|² + 8.|AC|²

-------------------------------------------------------------------------------------------

Výpočet délky |B′C′|² z trojúhelníku B′BC′ kosinovou větou:

|B′C′|² = |BB′|² + |BC′|² - 2.|BB′|.|BC′|.cos( BB′C )

cos( BB′C ) = -cos( CBA ) = -|BC|/|AB|

|B′C′|² = (2.|AB|)² + |BC|² + 2.(2.|AB|).|BC|.|BC|/|AB|

|B′C′|² = 4.|AB|² + |BC|² + 4|BC|²

|B′C′|² = 4.|AB|² + 5.|BC|²

-------------------------------------------------------------------------------------------

|A′B′|² + |B′C′|² + |A′C′|² = |AB|² + 8.|AC|² + 4.|AB|² + 5.|BC|² + |AC|² + 4.|BC|² =

= 5.|AB|² + 9.|BC|² + 9.|AC|² =

= 5.|AB|² + 9.(|BC|² + |AC|²) =

= 5.|AB|² + 9.|AB|² =

= 14.|AB|²

[přidat komentář]

Přidat svou odpověď

Přihlásit se k odběru odpovědí z této otázky:

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.

Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.