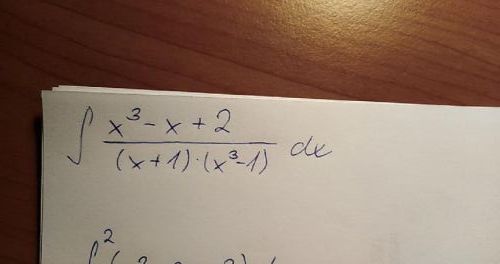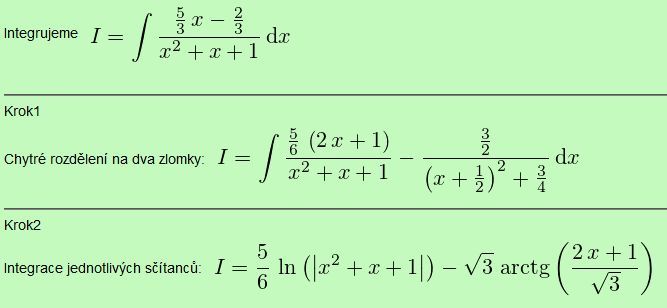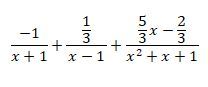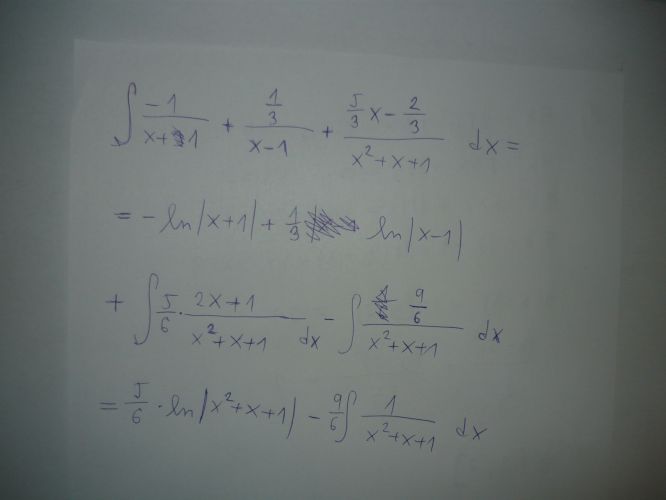Parciální zlomky

Tak, jak radí @kartaginec:

Tady jsou odkazy na soubory, kde je popis řešení těchto příkladů.

Možná tam najdete "návod". Kdyžtak na to večer kouknu, pokud to nespěchá.

gyza.cz/...

beda.8u.cz/...

rschwarz.wz.cz/...

Pamatuju si, že u těch členů, kde jmenovatel je s x na druhou, např. právě x²+x+1, nemůže být v čitateli jen konstanta , např. C, ale mělo by tam být Cx + D

To už jsem dlouho neřešil, takže v tomto nejsem moc "kovanej". Možná na to odpoví kartaginec nebo někdo další.Když ne, tak se na to večer podívám.

Ono to není až tak složité, spíš je to pracké - hodně počítání. No a přeci jen je to trochu komplikované, někdy, to množství počítání s tím souvisí.

K věci! Především bych upozornil, že rozklad se dělá pro zlomky, kde stupeň čitateleje nižšé než stupeň jmenovatele. Kdyby tomu tak nebylo (což není Váš případ), tak byste musel nejprve částečným vydělením problém na tento případ převést.

Další krok, který jste už úspěšně provedl, je rozložení jmenovatele na pireducibilní polynomy (dalo byu se říci na kořenové činitele, ale to není docela pravda, pávě například ten polynom x²+x+1 ještě nmení kořenový činitel, ale další rozklad by vedl na komplexní kořeny. Proto se tomuto polynomu říká ireducibilní.) Takže, rozklad (kekterému jste také došel, je

(x+1)(x³-1) = (x+1)(x-1)(x²+x+1)

No a teď je na řadě vlastní rozklad na parciální slomky. Tady má pravdu lopezz, že mnohočlenu x²+x+1 vodpovídá parciální slomek (Bx+C)/(x²+x+1). V tomto případě to je přesně tak, obecně by tomohlobát složitější, kdyby ty polynomy z rozkaldu vystupovaly ve vyšší mocnině, ale ti vynechám. Takže k nalezení rozkladu vyjdeme z rovnice

x³-x+2 =A/(x+1) +B/(x-1) +(Cx+D)/(x²+x+1)

ktrou vynásobíme tím jmenovatelem (x+1)(x-1)(x²+x+1).

Už je to dlouhé, zatím si počtštye, další pošlu později

Omlouvám se, zapomněl jsem nalevo napsat toho jmenovatele. tedy má být

(x³-x+2)/ [(x+1)(x³-1)]=A/(x+1) +B/(x-1) +(Cx+D)/(x²+x+1)

snad jste to pochopil.

Máte do správně:

Vzorec, na základě kterého se to asi dá spočítat, je na str. 4 souboru, na který je tento odkaz

is.muni.cz/...

V tom vzorci v tom souboru je tisková chyba. U toho a chybí x, je tam jen exponent

No a ted řešení: vynásobíme to tím jmenovatelem (x+1)(x³-1) a dostaneme

x³-x+2 = A*[(x-1)(x²+x+1)] + B*[(x+1(x²+x+1)] + (x+1) (x-1) (Cx+D)

Standardní postup řešewné je roznásobit a porovnat koefiucienty u stejných mocnin; dostaneme tak4 rovnicepro 4 neznámé. (Kdybyste poušil ten váš původní rozklad,měl byste tři neznámé a čtyři rovnice, což jke moc.)

Můžeme si to ale usnadnit, rovnice pladí prokaždé x, a dosadíme-li x = 1, respektive x = 0, dostanebe přímo rovnici pro B, respektive pro A.

Možná je to takto, ale nevím, co s dalším vzniklým zlomkem

Trovhu to rozepíšu.

To, co spočítal a uvedl @lopezz, mohu jen odsouhlasit. Snad jen doplním, že v tom výraze log(x²+x+1) mohu v logaritmu vynechat abs. hodnoty (ale nemusím), protože trojčlen x²+x+1 je stále kladný. Takže potřebuji integrovat výraz 1/(x²+x+1). To ostatně popsal xx, nicméně to taky popíšu Upravuji:

1/(x²+x+1) = 1/[(x²+x+¼) +¾]=1/[(x+½)²+¾]

Ve jmenovateli vytknu tu tři čtbrtiny, což je V3/2, kde jeko V3 jsem označil odmocninu ze tří:

1/[(x+½)²+¾] = 1/¾[{(2x+1)/V3}²+1]

No a teď už stačí použít substituci {(2x+1)/V3} = y, (2/V3) dx = dy.