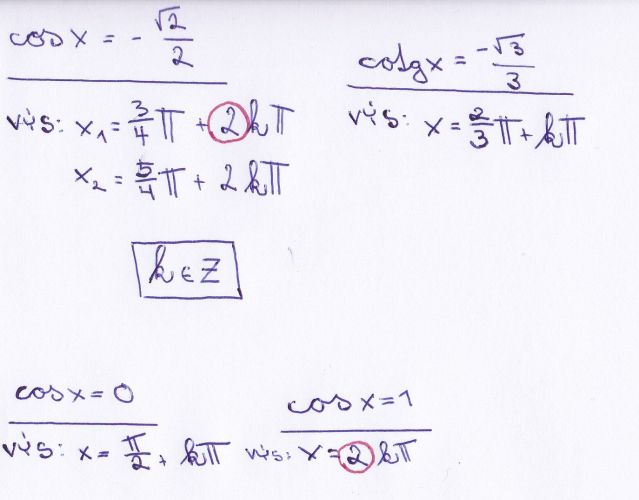Nejste přihlášen/a.
Dobrý den. Těžce se snažím pochopit goniometrické rovnice, nechápu zejména tuto věc: proč u některých zápisů konečných výsledků dopisujeme za výsledek periodu kπ a někde 2kπ. Opravdu tomu nerozumím, není třeba vysvětlovat podstatu do hloubky, matematiku jsem nikdy nechápala, jsem s tím smířená, nehodlám se jí v budoucnu věnovat. Potřebuji však rozpoznat, kdy napsat kπ a kdy 2kπ.
Omlouvám se všem matematikům jestli svou otázkou pohoršuji. ![]() Předem děkuji!
Předem děkuji!
PS: Jaký je pro laika nejsnadnější způsob řešení gon. rovnic? Vždy si načrtnu graf dané fce, někdy však špatně určím hodnotu stupně, v němž se zadaná hodnota protíná.
2x
Takhle obecně lze snad jedině říci, že kπ připočítáváme u funkcí, které mají periodu π (tangenta, kotangenta), 2kπ připočteme, když má funkce periodu 2π (sinus, kosinus), ale omo se to komplikuje, když jsou třeba základní řešení dvě, taky záleží na tom, co konkrétně hledáme, a vůbec. Raději si sem hoďte pár příkladů, které vám jsou nejasné, budeme se bavit o nich. To máte zrovna tak s otázkou, jak nejsnadněji řešit goniometrické rovnice, ono je jich více typů.
Snad takhle: za cíl si můžeme klást, najíd řešení v podobě sin x = y, nebo tan x = y a pod, a odsud určit x. No a tam je to tak, jak jsem psal na začátku. Ale zase ne tak úplně tak, to jsou ta dvě řešení. Pošlete nějaké příklady.
Přikládám namátkou vybrané příklady...
Vím, že rovnice se dají řešit vytýkáním, pomocí vzorců atd. Já mám nyní na mysli takovéto základní úlohy, jde mi jen o obecný postup - je dobré načrtnout si graf či zvolit jinou cestu?
Opravdu se omouvám, ale na dané učivo jsem chyběla, v pátek již navíc píšeme test.
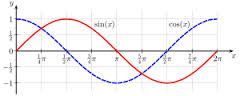
Tak to jsou vhodně vybrané příklady. A skutečně, pokud máme třeba cos = něčemu, bude tam k výsledku přičteno 2kπ, protože cosinus má periodu 2π. Opravdu je to vidět, když si uděláte prostý náčrtek. Na tom náčrtku se poríváte na jednu periodu, tedy o sinu je to ta vlnka, která jde z počádku nahoru, v x = ½π začne klesat, pro x = π je roven nule atd (na přiloženém obrázku je to ta červená křivka). Vy ovšem uvádíte kosinus, to je podobné, jen ta křivka na obrázku je ta modrá. Dále, jak správně uvádíte, se podíváte, kde ta křivka (tedy ten její kousek v intervalu je proťata hodnotou y , ve vašem případě
y = -odmocnina (2)/2 , vidíte, že jsou ty hodnoty dvě, cosinus se dále opakuje s periodou 2π, takže k těm dvěma výsledkům ořipočtete ke každému 2kπ; to jsou další hodnoty, které taky vyhovují. No, a se sinem by to bylo podobné.
Déle tam máte příklad s kotangentou, ta má periodu π, zato protože se nevlní, ale pořád klesá (tangenta by pořád rostle), hledáte to základní řešení v intervalu délky π (například, na obrázky 2 v intervalu (0,π) , dostanete jenom jedno řešení a peioda je π, ta přičítáte kπ.
Co vás možná mate, je, proč i u cosinu, u rovnice cosinus x =0, máte jedno řešení a přičítáte kπ a ne 2kπ. Ve skutečnosti máte i tady dvě ř"základní: řešení, totiž x = π/2 a x = 3π/2. Ke každému z nich přičítáte 2kπ, ale všimněte si, že to druhé řešení je od prvního vzdálené o π. Takže to x2 = x1 + π a místo abyste psala řešení ve tvaru x1 + 2kπ a x2 + 2kπ, tak ty dva zápisy spojíte do jednoh, a píšete řešení v podobě x1 + kπ.
Schválně si to zkuste: x1 = π/2, x2 = 3π/2 = π/2 + π, další řešení bude x1 +2π = π/2 + 2π, další x2 + 2π = x1 + 3π a tak dále.
Děkuji, už je mi to o něco jasnější. Procházela jsem sipříklady, poměrně úspěšně, akorát jsem se "zasekla" u již zde zmiňovaného příkladu, a to cosx=1. Nerozumím výsledku x=2kpí. Vždyť křivka kosinu protíná přímku v hodnotě 1 v bodě 0 a 2pí. Nějak to nedokážu pochopit...
To je trochu podobné jako s tím, když cos byl nula. Tady máte dva průsečíky, kterí jsou tentokrát vzdáleny o 2π, Takže od řešení x = 0 se odvíjejí další řřešení 0 +2kπ. Od x = 2π by se odvíjela další posloupnost, ael ono to x = 2π je vlastně už obsaženo v té první (pro k = 1), take s tou prcní splývá. Ono je jedno, jestli vezmete řešení 0 +1*2π, nebo 2π + 0*2π.
(Dalo by se to vysvětlit ještě z jiné strany, ale asi nemá smysl to komplikovat.) Zkuste si vyřešit rovnici sin x = 1, schvílně, co dostanete.
Dostanu x=pí/2 + 2kpí
Moc Vám děkuji za Vaši snahu a čas, určitě jste mi pomohl, nějaké drobné detaily mi sice stále viditelně unikají, ale myslím, že to nakonec zvládnu.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.