Jak převedu tangens na úhly?

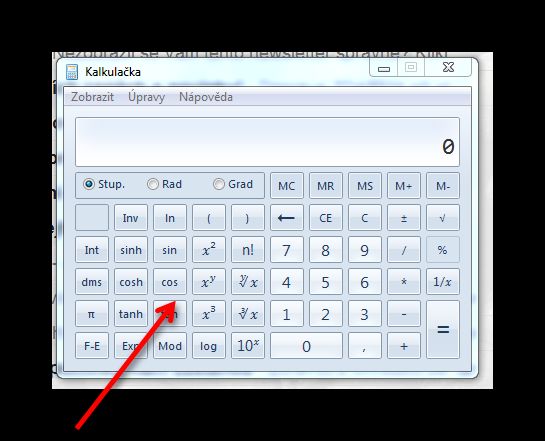
V zásadě je to tak, jak píše ¨@zvidavaajanca. Asi stojí za to, upozornit na dvě (až tři) věπsím nejprve stisknout tlačítko inverzní funkce (obvykle inv) a až pak tan.

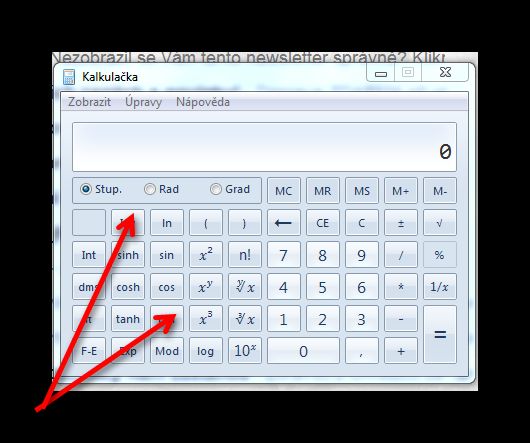
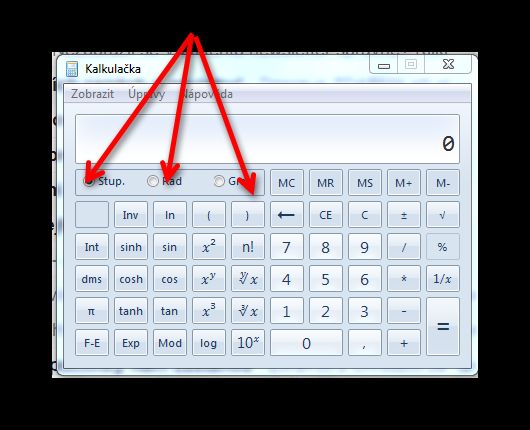
2. Na přiloženém obrázku (ten poslední, je to obrázek vědecké kalkulačky z woken) si všomněte tří tlačítek _ stup, rad, grad _, které určují, v jakých jednotkách dosazujete úhle, respektive v jakých jenotkách vám vyjde. Grad jsou klasické stupně (třeba pravý úhel je 90°), rad označuje míru obloukovou (pravý úhel je ½π) a grad je jednotka, která odpovídá rozdělení plného úhlu na 400 dílků, takže pravý úhel je 100^g. Tu poslední jednotky asi moc používat nebudete, a ještě upozorňuji, že na různých kalkulačkách mohou být určité odchylky, třeba gon místo grad, a tak. Přiložené obrázky jsou, jak říkám, z kalkulačky, která je ve windows, a to v její vědecké podobě.

3. Když už jste na VŠ, jest upozorniti, že tangenta není prostá a inverzní funkce tedy neexistuje. To, co zjišťujete na kalkulačce, je tzv. arkustangenda, tedy to řešení rovnice tan x = y, které leží v základním intervalu, v případě radiánů mezi -½π a ½π. Všechna řešení této rovnice dostanete, když k tomu základnímu připočtete libovolný celý násobek periody (v radiánech jde o násobek π)

Z oraktického hlediska jsme to vyřešili. Snad jen dodám, že krom kalkulačku lze použít i tabulky, což ovšem vyžaduje znát určité triky, ale o tom mluvit nebudu.

Zůstává ovšem otázka, jak to spočítat, konec konců ty tabylky nespadly z nebe a kalkulačka to nějak počítá, nemá v sobě naládované tabulky. To je ovšem otázka, která se týká nejen výpočtu úhlu z tangenty, ale i třeba inverzně, výpočtu tangenty z úhlu, obecně goniometrickýcc a cyklometrických funkcí. To už je skutečně vysokočkolská matematika ´. Nějaký "uzavřený" vzoreček, jak si ho asi představujete vy, tj. nejspíš by vás uspokojila nějaká, třeba velmi složitá kombinace sčítání, odčítání, násobení, dělení, odmocňování, do které byste dosadila a vypadla by hledaná hodnota, jaksi nenajdete. Tyto funkce lze počítat jedině přibližne (mimochodem, to se vlastně týká i odmocniny z obecného kkladného čísla, jenže tam nám to tak nepřijde), například pomocí Taylorových řad, nebo jiných metod numerické matematiky. To je velmi široký obor, kterým se tu zabývat nemůžeme, pro představu uvedu, jak by se dal počítat sinus. To je relativně jednoduchý postup, počítáme ho jako součet nekonečné řady

sin x = x - (x³)/3! + (x⁵⁾/5! - (x⁷)/7! + ..., čím více členů sečteme, tím přesnější bude výsledek. Jiné funkce lze počítat podobně, jen příslušné mocninné řady jsou složitější a někdy je vhodnější volit jiné postupy.

Vlastně, pro arctangentu bychom mohli použít vzorec

arctan x = ∫^x dt/(1+t²)

(integrál od nuly do x). Ale jak spočítat ten integrál?

Buď pomocí arkus trngenty, což je kruh, nebo přibližnými metodami, podobně jako Taylorovu řadu.