Dvě myši byli zavřené ve svém výběhu, kterým byl uzavřený tunel, ajehože chodby tvořily strany čtverce. Oba dva čtverce měly společný střed, strany byly dlouhé 4 a 2 m. Měnší byl vůči tomu většímu otočen o 45°. První myš byla v pravém horním rohu horního rohu, druhá v horním rohu menšího výběhu. Myši běhali stále dokola po hranici výběhu rychlostí 1 m/s. Myš z většího výběhu pobíhala po směru hodinových ručiček, myš z menšího proti směru. Jak nejblíže se k sobě můžou dostat a za jak dlouho nejdřív se to stane?
0x
Podilam nakres situace. Puvodni mysi: cerna a modra. Fialove jsou body, ve kterych jsou mysi, kdyz si jsou sobe nejblize.
Oranzova je jejich nejmensi vzdalenost: Ta je: 2 (vzdalenost strany vetsiho ctverce od stredu) minus polovina uhlopricky mensiho ctverce, to je 1/2 √2 * 2 = 2 - √2 = 0,7
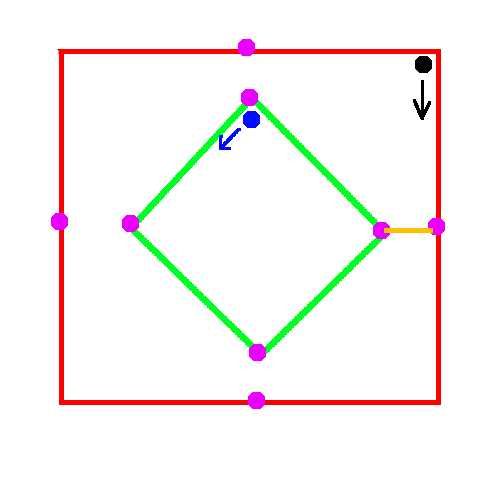
- vpravo v casech: 2 + 16k (dobehne tam poprve za 2 sekundy a pak kazdych dalsich 16 sekund az obehne cele kolecko)
- dole v casech: 6 + 16k
- vlevo: 10 + 16k
- nahore: 14 + 16k
- horni: 0 + 8n
- vlevo: 2 + 8n
- dole: 4 + 8n
- vpravo: 6 + 8n
Modra mys bude ve fialovych bodech v techto casech:Budeme tedy hledat nejmensi spolecny cas, pro ktery se mysi potkaji v kazdem fialovem bode a pak vybereme ten fialovy bod, ve kterem se potkaji nejdrive.
Napr. pro fialovy bod vlevo budeme hledat spolecny nasobek cisel (10+16k) a (2+8n)
10+16k = 10, 26, 42, 58, ...
2+8n = 2, 10, 18, 26, ... - horni: 0 + 8n
Dopocitam to, at to tady nevisi takhle rozpocitane do pulky. Treba to nekomu pomuze prijit s efektivnejsim resenim.
Z vypoctu vyse plyne, ze mysi se poprve setkaji v levem bode za 10 sekund. Cerna mys tam dorazi pri svem
prvnim obihani kolecka, ta modra uz za sebou bude mit kolecko a ctvrt v tom mensim ctverci.
Pro horni:
14+16k = 14, 30, 46, 62, 78, 94, 110, 126, 142, 158, 174, ...
0+8n = 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 142, 150, 158, ...
Mysi se tedy nahore potkaji poprve po 142 sekundach.
Pro pravy:
2+16k = 2, 18, 34, 50, 66, 82, 98, 114, 130, 146, 162, 178, 194, 210, 226, 242, 258, ...
6+8n =6, 14, 22, 30, 38, 46, 54, 62, 70, 78, 86, 94, 102, 110, 118, 126, 134, 142, 150, 158, 166, 174,
182, 190, 198, 206, 214, 222, 230, 238, 246, 254, 262, 270, ...
Tady me prestalo bavit hledat nejmensi spolecny nasobek tech dvou cisel hrubou silou (jestli vubec existuje - nad tim se jeste budu muset zamyslet. Navic me ted napada, ze se tomu asi neda rikat "spolecny nasobek", ale spise shodny clen posloupnosti). I kdyby to stejne cislo bylo "za rohem", tak v nejlepsi pripade bude kolem 280, coz je porad vetsi nez tech 10 sekund, za ktere se mysi poprve potkaji v levem bode, cili nas tento pravy bod nezajima.
Dolni bod:
6+16k = 6, 22, 38, 54, 70, 86, 102, ...
4+8n = 4, 12, 20, 28, 36, 44, 52, 60, 68, 76, 84, 92, 100, 108, ...
Opet vidime, ze spolecny cas, kdy se tam potkaji, bude v nejlepsim pripade neco pres 100, coz je opet dele nez tech 10sekund v levem bodu, takze nemusime presne hledat, v jakem case se poprve v dolnim bodu poprve potkaji.
Vysledek je, ze nejblize se k sobe mysi dostanou na 0,58 metru a bude to za 10 sekund od vybehnuti.
Tak jeste jedna oprava: ![]() Ta chyba neni v nasobcich 14+16k, ale v 0+8n a spolecny cas tak neni tech 142, ale vice. Opet konkretni cas je nezajimavy, protoze je vetsi nez tech 10 sekund v levem bodu, ktery jsme uplne nahodou spocitaly jako prvni (opravdu v tom z moji strany nebyl zadny umysl).
Ta chyba neni v nasobcich 14+16k, ale v 0+8n a spolecny cas tak neni tech 142, ale vice. Opet konkretni cas je nezajimavy, protoze je vetsi nez tech 10 sekund v levem bodu, ktery jsme uplne nahodou spocitaly jako prvni (opravdu v tom z moji strany nebyl zadny umysl).
0x
Cim vice casu travim premyslenim o teto uloze, tim vice me fascinuje.
Jakkoliv se zda jednoducha, v obecnem pripade se jedna o netrivialni ulohu. Napriklad jaka je minimalni vzdalenost tech mysi v case pod 10 sekund? Jak udelat graf jejich vzajemne vzdalenosti v libovolnem case? Setkaji se vubec nekdy v jinem nez v tom levem bode? Jak by se uloha zmenila pro ruzne rychlosti mysi? Odlisne vychozi body? Obecnejsi natoceni mensiho ctverce?
Zajimave. Velice zajimave.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.