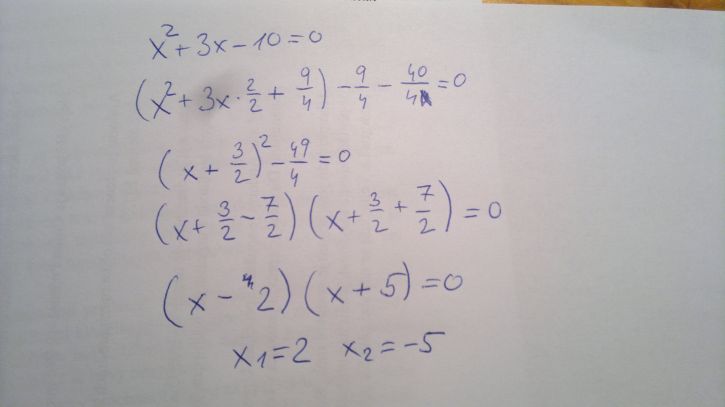Kvadratické funkce - vrcholové body

Dobré jako výpočet kořenů, ale dostaneme odsud i vrchol paraboly: vrchl paraboly s rovnicí

y = x²

je počátek (nebo to lze říci i opačně, rovnice poraboly s vrcholem v počátku je y = x²) a parabola

y =(x-a)² +b

má vrchol posunutý do bodu x-a = 0, y = b a tn je tedy roven [a,b]

Je pravda, že jsem ve svém obecném popicu vlastně mluvil (aniž bych to řekl) pouze o parabolě rozevřené nahoru, úplný popis by byl, že parabola

y =±(x-a)2 +b

má vrchol [a,b] a je rozevřené nahoru (vrchl má dole) nebo dolů podle znaménkapřed kvadratickým členem. Naše parabola má po úpravě rovnici y = -(x+1,5)² + 12,25, dle výpočtu, který provedla @elisa24 (která ovšem řešila rovnici, takže pro zjednodušení změnila znaménko - vynásobila rovnici mínus jednou), což odpovídá Lukemu.

A ještě dvě až tři poznámky na okraj:

1) pokud chci spočítet kořeny, mohu od okamžiku, kdy jsem rovnici upravil na tvar (x-1,5)² - 12,25 = 0 postupovat tak, že napíšu (x+1,5)² = 12,25, (x+1,5) = ± sqrt 12,25 = ±3,5 a dostanu x1 = -1,5 + 3,5= 2, x2 = -1,5 -3,5 = -5, což je tvar, odpovídající výpočtu pomocí determinantu

2) kořeny x1 = 2, x2 = -5 lze při troše praxe uhádnout zpaměti na základě Vietových vzorců (víme, že jejich součin je -10, což může být 1*10 nebo 2*5, přičemž ovšem u jednoho z těch čísel musí být mínus, a z těchto čtyř možností snadno vyberete tu, pro kterou součet je -3 (samosřejmě pokut taková možnost existuje, tedu bokud příslušná kvadratická rovnice má celočíselné kořeny.

3) metoda doplnení na čtverec funguje i v případě, kdy rovnice reálné kořeny nemá (parabola neprotíná osu x). (Po pravdě, jistým trikem bychom ji mohli pro nalezení vrcholu paraboly použít i tak, stačilo by k rovnici přičíst či od ní odečíst vhodné číslo tak, aby kořeny měla; pak x-ovou souřednici najdeme Lukeho metodou a y-novou pak dostaneme, když se vrátíme k původní rovnici.

Oprava: v jednom místě jsem zapoměl opravit kvadratický člen, který má bát -(x+1,5)². Tak aby bylo jasno.