Dobrý podvečer,
ráda bych se zeptala, zda by mi někdo neporadil s tímto planimetricky zaměřeným úkolem.
Je dána kružnice k a bod A jako její vnější bod. Sestrojte sečnu kružnice k tak, aby procházela bodem A a pro její průsečíky X,Y s kružnicí platilo |AX|=2|AY|.
Probírala sem příklad se známými a kamarád ho řešil pomocí rovnoběžníku, ale to jsem moc nepochopila jak.
Za jakékoli rady Vám budu vděčná.
Děkuji
0x
Úlohu lze řešit pomocí mocnosti bodu ke kružnici. Platí:
|AX| ⋅|AY| =|MT|^2
2|AY|⋅ |AY| = |MT|^2
|AY| = |MT|/√2 = |MT|⋅√2/2
Bod Y bude průsečík kružnice o středu M a poloměru r = |MT|⋅√2/2 s danou kružnicí k.
Místo bodu M má být A
|AX| ⋅|AY| =|AT|^2
2|AY|⋅ |AY| = |AT|^2
|AY| = |AT|/√2 = |AT|⋅√2/2
Bod Y bude průsečík kružnice o středu A a poloměru r = |AT|⋅√2/2 s danou kružnicí k.
Děkuji, toho že to bude něco s mocností bodu ke kružnici jsem se obávala. :D protože si to moc nepamatuji. děkuji ještě jednou 
Můžu se ještě zeptat jak bych to tedy narýsovala? jaký by byl postup?
doplněno 09.01.14 22:09:Musela bych to řešit přes body dotyku? abych zjistila délku AT? a mohlo ji použít pro získání rozměru poloměru?
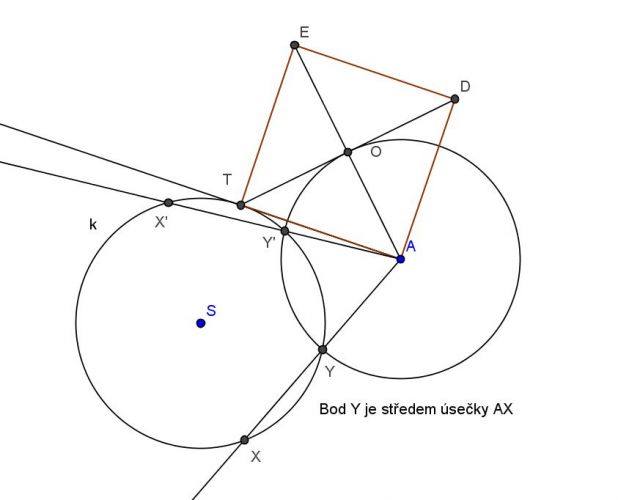
1) Z bodu A sestrojíme tečnu ke kružnici a bod dotyku T.
2) Nad úsečkou AT sestrojíme čtverec a jeho střed O.
3) Sestrojíme kružnici (A; r = |AO|).
4) Průsečík této kružnice s danou kružnicí je bod Y. Sečna je pak přímka AY.
V mém případě má úloha dvě řešení. Je-li bod více vzdálen než je |AO| od dané kružnice, úloha nebude mít řešení. V případě, že se kružnice dotkne dané kružnice, bude mít úloha jedno řešení.
0x
Řešení x je perfektní. Já jen dodám, že podmínkou řešitelnosti (v podobě ověřitelné dřív, než začnu konstruovat tečnu) je to, aby vzdálenost bodu A od kružnice nebyla větší než dva její poloměry (čili než její průměr), a že správnost konstrukce plyne i z Ekleidovy věty ve tvaru a2 = c*ca: vskutku, mocnost bodu A ke kružnici je rovna kvadrátu délku tečny, tedy |TA|2, a ten je, podle Eklidovy věty, aplikované na trojúhelník TAE, roven |AE|*|AO|. (No a střed čtverce, jak řečeno výše, půlí úhlopříčky.)
Jinak vysoce hodnotím perfektní obrázek a rád bych dal x bod, takhle aspoň 
.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.