Prý se o derivacích říká, že je umí spočítat každá opice, jak je to jednoduché. Jenomže já opice nejsem. Prosím, program ukázal tento výsledek. Jsem úplně mimo. Děkuji.
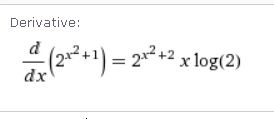
0x
Derivace exponenciální funkce je (ax)´ = ax ln a.
V našem případě se navíc jedná o složenou funkci. Takže derivujeme vnější funkci a násobíme ji derivací vnitřní funkcí. Logaritmus je přirozený.

Při násobení mocnin o stejném základu se exponenty sčítají: ar ⋅ as = ar+s
V našem příkladě 2x^2 + 1 ⋅ 2 = 2x^2 + 2
První exponent: x2 + 1, druhý exponent 1. Součet je (x2 + 1) + (1) = x2 + 2.
0x
To jsem zvedavy, kdo se jako prvni vyjadri k tomu slonovi v mistnosti, ktereho zatim vsichni prehlizi, tedy ze ve vysledcich je "log", ale vyslo "ln".
Chapu, ze Americani nepouzivaji "ln", ale nemeli by pak u toho "log" napsat "e"?
Je ihned patrné, že tazatel použil WolframAlpha, kde je poznámka, že se jedná o logaritmus přirozený. I já upozorňuji, že se jedná o přirozený logaritmus.

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.