Riemannův integrál

Tak především, jistě je ván jasné, že tea "definice" není vlastně definice, ale spíše jakési vysvětlení, názornější, než by byla přesná defonice, za cenu jistých něppřesností nebo neúplností, ale to teď není podstatné.

K prvnímu příkladu, po pořadě:

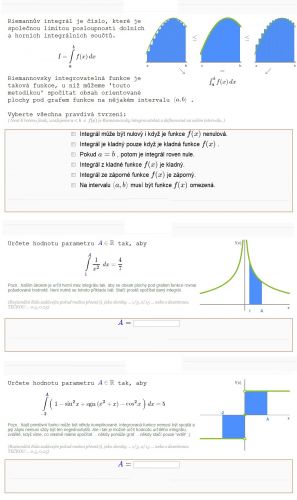
1. pravda (funkce může být někde kladná a někde záporná a to tak, že se tyto části vzájemně vykompensují, nebo názorně, plocha pod kladnouo částí funkce je v absolutní hodnotě rovna ploše nad zápornou částí ? _ cum grano salis

2. nepravda (stačí, když "kladná plocha" převáží tu zápornou

3. pravda

4. pravda (s tou podmínkou, že a < b)

5. dtto

6 pravda (tedy pokud mluvímě o klasické definici vlastního Riemannova integrálu, a pokud doplnímé "má-li untegrál existovat".)

Druhý a třetí příklad řešit nebudu. Druhý je prostě výpočet integrálu, to jistě umíte, a třetí sice vypadá komplikovaně, ale po úpravě se výrazně zjednoduší a ten graf je výrazná nápověda; tedu pokud víte, co znamené sgn a umíte řešit nerovnosti).

Takže to 2 a 3 si zkuste a v případě, že budete potřebovat více poradit, tak se ozvěte.

Něco mi vypadlo, doplňuji a upřesňuji):

4. pravda (s tou podmínkou, že a < b a funkce je f spojitá; co platí bez problémů i pro nespojité funkce, je to, že pro f ≥ 0 je i integrál nezáporný. S ostrou nerovností je to složitější, nicméně bez těch dodateěných předpokladů by odpověď měla být nepravda).

Zase se mi ten doplněk vložil neúplně a nedává smysl. Vrátím se k tomu ještě, ale ono je to jemné upřesnění, takže není až tak podstatné. Zatím se tím netrapte.