Nejste přihlášen/a.
0x
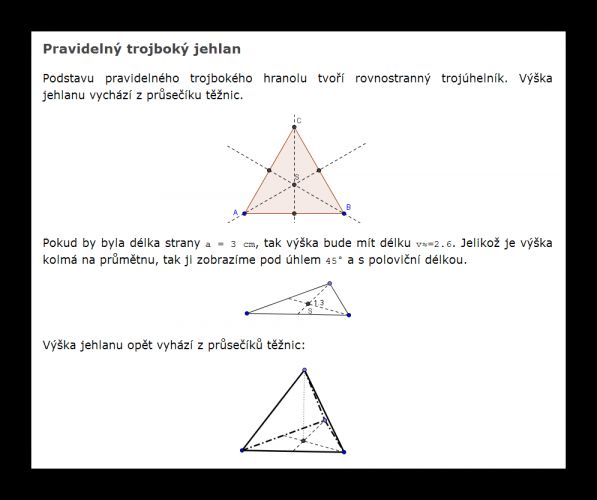
Na tomto promítání není v zásadě nic těžkého. Nejdříve si musíme určit průmětnu. Útvary v této rovině (nebo rovnoběžné s touto rovinou) se zobrazují ve skutečné velikosti a ve skutečných úhlech. Útvary kolmé na průmětnu se promítají pod úhlem 45° a poloviční délkou (viz maths.cz/...)
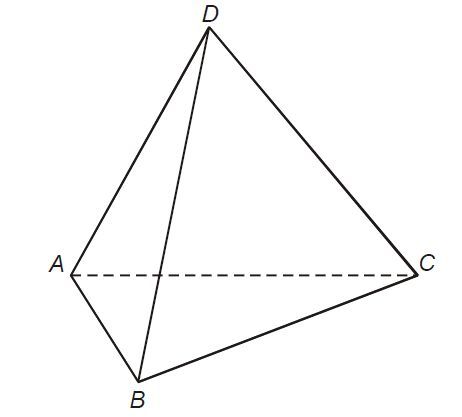
x namaloval výsledek. Co se týče rozměrů, zynovu odkazuji na výše zmíněný úvod do stereometrie. Odstavec, týkající se pravidelného trojbokého jehlanu (čtyřstěnu) sem zkopíruji jako obrázek.
doplněno 09.12.13 10:45:Tahle konstrukce je vhodná pro obecnou výšku. Váš jehlan je ovšem speciální, jeho hrany jsou všechny stejné, ať jde o podstavu či boční stěny. Jistě dovedete jeho výšku zkonstruovat jako výšku trojúhelníka, jehož jedna strana je rovna hreně jehlanu a druhé dvě jsou výšky podstavového trojůhelníka.
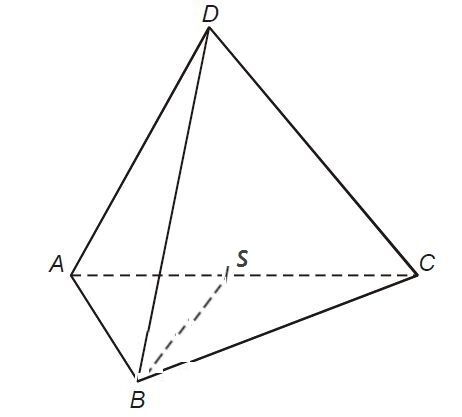
To jsem se pokoušel naznačit v doplnění, Takže podrobněji:
Použiji obrázek od x, do kterého jsem přimaloval bod S, což je střed úsečky AC. (viz obrázek.) Trojúhelník SBD představuje svislý řez jehlanu (to je doufám jasne) a tělesová výška je rovna jeho výšce. Takže stačí si ho nakreslit vedlev jezkreslené podobě. K tomu si všimnum že strana BD je hrana jehlanu, strana BS je pak výška základny a srtejnou délku má strana SD, Stačí to takhle?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.