Nejste přihlášen/a.
0x
Chtělo by to upřesnit dotaz, integrál se zlomkem by mohl být například integrál z konstantní funkce y = 1/4. A taky možná by to chtělo napsat, jestli vám jde o určitý či neurčitý integrál. Pokud vás zajímá neurčitý integrál (primitivní funkce) z racionální lomené funkce, zde se obvykle začíná částečným vydělením a následným rozkladem na parciální zlomky. Nicméně to není k zodpovězení na dva řádky. Zkuste předhodit konkrétní příklad, který by vás zajímal; zatím přidám obrázky s textem řešení jednoho takového příkladu.
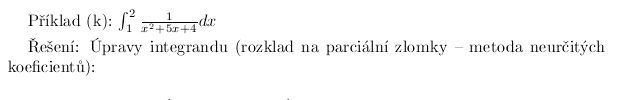

Uf, to je mazec. Pokusím se nahrát fotku s příklady.
doplněno 02.12.13 18:02:Četl jsem cosi o substituční metodě, snad to nebude na tohle. Nejsem přece vědátor!
A díky!
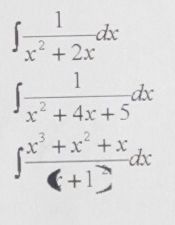
Substituční metoda existuje, ale není to specifická metoda na integrály s racionální funkcí. Někdy se pro ne hodí, někdy ne, a někdy se hodí pro jiné typy integrálů, to je případ od případu. Prostě to chce praxi, aby člověk věděl, kdy co použít.
Ty příklady, které jste uvedl, nejsou složité, já řešení nascenuji a přidám jako obrázek, aspoň u těch prvních dvou. Substituci u nich nakonec použijeme, ale ve velmi jednoduché formě. Ten třetí ale jaksi nedovedu rozluštit; co je to tam ve jmenovateli:
doplněno 02.12.13 19:02:Předběhl mne x, nic jiného bych vám neporadil.
doplněno 02.12.13 19:31:Snad jen bych do toho necpal program maxima, to jsou prostě základní vzorečky pro integraci (jsou to vlastně vzorce pro derivaci čtené zprava dolevaú, prostě tabulky promitiivních funkcí, Nenechte e tím zmást.
0x
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.