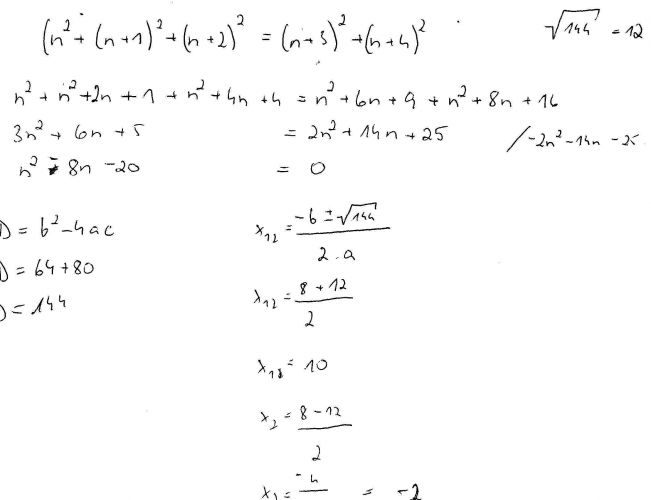Dobrý den všem ,
chci poprosit o radu jak počítat a jak postupovat ( výsledek není důležitý , spíše to potřebuji pochopit ) u dvou příkladů . Ze školy jsem už hodně dlouho a tohle už fakt nedávám .
Děkuji za vysvětlení a případné rady .
5x
V prvním případě bych si první z těch celých čísel označil třeba n. "Po sobě jdoucí" znamená "i jedničku větší". Takže druhé číslo bude n+1, třetí n+2 a tak dále. Podmínku úlohy zapíšu do rovnice (n2 + (n+1)2 + (n+3)2 = (n+4)2 + (n+5)2) , což je kvadratická rovnice pro n
Ve druhém případě bych spočítal součet druhých mocnin čísel 3,4 a 5 a načel bych koeficient, kterým je třeba je násobit, (čímž jejich poměr byde zachovánú, aby vyšlo to, co chci-
Díky moc za radu , nyní se to budu snažit pochopit :D . Ještě dotaz , kam se podělo u prvního příkladu n+2 a rovnou je tam (n+3 ) to celé na druhou . Pro vás je to sranda ,ale já jsem úplně vedle . Děkuji
2x
Oba priklady se nechaji resit napr. jako soustavy rovnic.
-
U prvniho prikladu je to pet rovnic pro pet neznamych:
Plati, ze
a2+b2+c2=d2+e2
a zaroven, ze
a+1=b
b+1=c
c+1=d
d+1=e
-
U druheho pripadu jsou to tri rovnice pro tri nezname:
Plati, ze
a2+b2+c2=1250
a zaroven, ze
a/b=3/4
b/c=4/5
0x
Tri po sobe jdouci cela cisla jsou: n, n+1, n+2
soucet jejich druhych mocnin je: n2 + (n+1)2 + (n+2)2
Soucet druhych mocnin po nich nasledujicich cisel: (n+3)2 + (n+4)2
Rovnice upravis podle vzorce (a+b)2 = a2 + 2ab + b2 a vyresis. Jako kontrolu vis, ze "n" ti musi vyjit cele cislo (bylo to v zadani).
Podobne se bude resit druhy priklad.
perfektní , děkuji, jak jednoduché , když se to ovládá
doplněno 07.01.14 10:55:ještě bych poprosil , stejně pěkně popsat druhý příklad .
Díky
Po uprave pomeru, ti vyjde: a=3b/4; c=5b/4
Dosadis do te kvadraticke rovnice a spocitas "b". Z neho pak ze zlomku a predchozi radce urcis a,c.
tak tohle bohužel nechápu ![]() .
.
jak upravím poměr , kde se vzalo a=3b/4 , c=5b/4
první příklad jsem pochopil ,ale tohle né ![]() .
.
Děkuji za trpělivost
Co ti nevyslo? Vysla ti dokonce 2 reseni: n=10 a n=-2 ![]()
Zadani tedy vyhovuji posloupnosti cisel: 10,11,12,13,14 a -2,-1,0,1,2.
Pro jistotu jeste udelej zkousku (dosad do zadani).
Ať nezakládám nové téma . Prosím o radu jak na tento příklad
Součin dvou po sobě následujících přirozených čísel je o 55 větší než jejich součet. Která to jsou čísla . Zase mi nejde o ty čísla ale o logickej postup . Moc děkuju za radu
n x ( n + 1) ... nevím n+(n+1)
moc díky, stejně dělám někde chybu , protože mi D vyšlo 223 a mělo by vyjít 225 ![]() . I tak díky snad to dohledám
. I tak díky snad to dohledám
zase znamínko , sakra toková hloupá chyba :D .
Ještě jednou díky za vaše rady
a ještě jedna úloha - součet druhých mocnin po sobě následujících přirozených čísel je o 24 menší než druhá mocnina součtu těchto čísel .
doplněno 10.01.14 14:52:n na druhou + ( n+1) to celé na druhou = (n+n+1) to celé na druhou -24
asi hloupost , že
Co vám vychází? Mně vyšly dva kořeny: n1 = 4, n2 = _ 3
doplněno 10.01.14 16:58:Pardon, opačně. Rovnice je (n+4) (n_3)= 0, kořeny tedy n1=_4, n2=3. (No a podmínka, že hledáte přirozená čísla, samozřejmě vyloučí tu -4.
n2 + n2 + 2n + 1 = 4n2 + 4n + 1 - 24
2n2 + 2n -24 = 0
n2 + n - 12 = 0
D=1-4.1.(-12) = 49
n1,2= (-1 ± 7)/2
n1= 3
n2= -4
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.