Nejste přihlášen/a.
Prosím, zasekl jsem se na takto jednoduchém příkladu.
Limita (x-2)/x,,,,, x se blíží limitně nule. DĚKUJI!
2x
si myslím, že by se dalo použít lHospitalovo pravidlo : Limitu zderivujte. Co zbude po derivaci, je výsledek.
doplněno 22.11.13 12:11:Uf. Doufám že si to pamatuji dobře. Podmínkou LHospitalova pravidla je limita typu 0/0 nebo nekonečno/nekonečno. Ve škole nám povídali, že když pochopíte jak se tyto příklady vlastně počítají, pak znáte výsledek ještě dříve, než dočtete zadání. Výraz napište jako zlomek, zderivujte odděleně čitatele i jmenovatele. Když má X mocninu, pak derivujte tak dlouho, dokud úplně nezmizne. Co zbude, je výsledek.
Kdybyste měl ve zlomku (3x²+50x)/(100x-1000), pak můžete klidně vystřelit od pasu, že výsledek je 6.
doplněno 22.11.13 16:06:poslyšte rádci. Zas jako obvykle všichni víte co je špatně, ale taky jako obvykle vám chybí řešení otázky. Marně tu nějaké hledám.
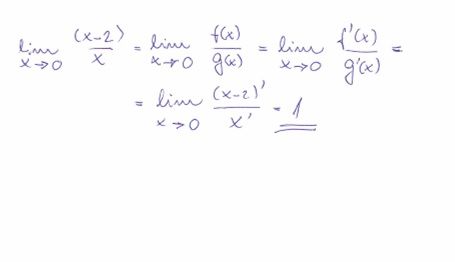
Limita v tomto případě neexistuje a L’Hospitalovo pravidlo na tento příklad nelze aplikovat - viz graf:
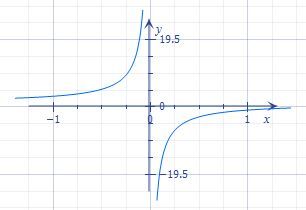
Hned jako první odpovídá x"
Limita neexistuje:
a tuto odpověď rozvádí v dalších příspěvcích. Nicméně, je pravda, že nenapsal explicitně, čemu že se rovnají ty jednostranné limity, i když uvnitř jeho odkazů to je. Tak si dovolím napsat to ještě sem, přímo do vlákna:
Limita (x-2)/x = -∞ když x se blíží limitně nule zprava
Limita (x-2)/x = ∞ když x se blíží limitně nule zleva
Vlastně by se to dalo vyčíst i z příspěvku Luke127 a následné opravy, ale, pravda, je to tam poněkud zašifrovaně.
A když už se tedy o tom bavíme, tak obrat
Limitu zderivujte.
(ještě napsaný tučnými písmeny) je tak trochu nesmyslný.
doplněno 22.11.13 17:06:
Jina rádce x, krom toho, že otázku zodpověděl hned v prvním příspěvku, odpověděl i v odpovědi dnes 12:40. Možná by to chtělo trochu zdrženlivosti.
A vlastně, když o tom tak přemýšlím, není to poslední tak nemástná poznámka. Když tam to řešení nevidíte vy, o to pravděpodobnější je, že ho tam nevidí tazatel. Ale tazatel už nepíše, takže to nemoho posoudit, nicméně měl by. Uvidíme.
doplněno 23.11.13 12:20:nemístná poznámka
0x
Jak pise figurek. Pouzit LHospitalovo [lopitalovo] pravidlo.
Citatel i jmenovatel jsou funkce (jde o limitu podilu dvou funkci), kde kazdou funkci zvlast zderivujeme a tedy vznikne limita podilu derivaci puvodnich funkci.
Musi byt splnena pdminka, ze funkce ve jmenovaleti i jeji derivace musi byt ruzne od nuly (kvuli deleni nulou) a ze limity obou funkci (v citateli i ve jmenovateli) jsou bud obe nulove nebo obe nevlastni (po spocteni jejich limit vyjde nula nebo nekonecno).
-
Obe podminky jsou zde splneny, takze pravidlo lze pouzit.
LHospitalovo pravidlo se na tento příklad nedá použít, neboť se nejedná o typ 0/0. Viz např.: aristoteles.cz/...
Ze se nejedna o typ 0/0 je pravda. Jedna se totiz o typ nekonecno/nekonecno. Coz je druha moznost te podminky. Jak mas konec koncu i uvedeno v tom Tvem odkazu.
Pouzit tedy pravidlo lze.
A jo. Omlouvam se. Ja nevim proc sem byl presvedceny, ze se x blizi k nekonecnu a ne k nule.
Spatne sem cet zadani. Moje chyba.
0x
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.