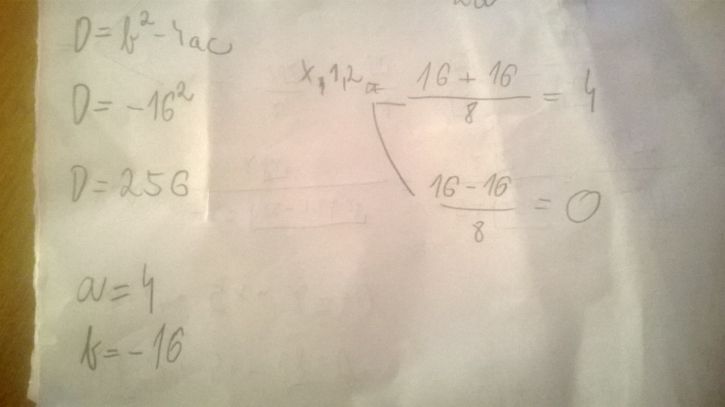0x
Pokud je to rovnice typu ax² + bx + c = 0, tak řešení je akela.mendelu.cz/...
(pro rýpaly: dotaz je jak vyřešit, ne jak se to naučit)
0x
Mnozí ti radí což hraničí až s podvodem.Diskriminant je jedna cesta ovšem chce si to pamatovat vzorečky. Tato cesta se nechá zapamatovat.
ax²+bx+c celou rovnici vydělíme "a" a zbavíme se absolutního členu u mocniny když pak b/a=m
umocníme si dvojčlen (x+(m/2))² v podstatě výsledek se bude shodovat s původní rovnicí po vydělení, až na absolutní člen, takže k němu přičteme či odečteme další hodnotu, aby výsledek odpovídal zadání. Upravíme na tvar kdy odmocníme součet těch dvou absolutních členů
(x+(m/2))²-p² a tento výsledek řešíme podle známého vzorce (a²-b²)=(a+b)(a-b)
A kořeny té rovnice jsou, když hodnota prvního nebo druhého dvojčlenu je rovna nule
0x
Tak tady jsem vypočítal úkol a zajímalo by mě jestli je to dobře hlavně do b jestli je -16 nebo se to bere bez - jako +16. Díky 
A výsledek se ještě nějak extra zapisuje nebo toto je celý?
Pak by mě zajímalo když v odmocnině je třeba 7 jak se odmocňuje? To by tam vznikaly nějaký divný čísla :o
Rozumím-li dobře, je c = 0, čili řešíš rovnici
4x² - 16x = 0,
je to tak? Pokud ano, musíš do zadaní to c = 0 zadat, to není tak, že v té rovnici c není, ono tam je, ale je nulové. Pak je to skoro dobře, respektive docela dobře, jen se špatným zápisem po cestě. . Ptáš se, jak se bere to b, jestli s mínusem nebo bez něj. Bere se s mínusem, ale i s tím mínusem se umocňuje, tedy b² = (- 16)² = 256. Takže diskriminant máš dobře, akorát ty tam máš dvě chyby, které se kompenzují: píšeš D = -(16²) = 256 (tu závorku tam nemáš, tu jsem tam přidal, abych zdůraznil. co mám na mysli). Prostě v prvním kroku máš mínus, které tam nepatří, a ve druhém kroku ho zrušíš, aniž bys k tomu měl důvod, takže nakonec se dostaneš ke správnému výsledku.
Lze k tomu dotat ještě více, ale nejdřív bych rád věděl, jestli jsem správně vytypoval rovnici, kterou řešíš, tedy jestli máš c = 0.
(Ještě k té odmocnině ze sedmi: tam, pokud to chceš řešit numericky, opravdu nevyjdou hezká čísla. Běžně se to ale nechává v naznačené podobě, tedy jako "odmocnina ze sedmi", jednak je to lepší pro případné další úpravy, a jednak si tím do budoucna ponecháváš možnost, s jakou přesností (na kolik desetinných míst) to chceš spočítat. Jakmile to jednou numericky odmocníš, zavádíš do výsledku zaokrouhlovací chybu, se kterou už do budoucna nic neuděláš.)
Jsou lidi kteří se drbou pravou rukou za levým uchecem. Taky to jde. Takže spíš myslet, než diskriminant. Pokud by šlo o uvedenou rovnici, vytknu "x" a jak "x" či dvojčlen v závorce se musí rovnat nule.
Jistě. To je to, o čem jsem chtěl mluvit po potvrzení tvaru rovnice.
V těch zadaných (které jsi pro přehlednost opsal přímo do textu, aby se nemusel pracně otvírat špatně zadaný odkaz (
) není, ani postup žádné z nich neodpovídá, to je důvod mého požadavku. Teď je na tahu tazatel, asi se ozve někdy večer.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.