Ahoj, mám dotaz... když chci sílu graficky zobrazit, jak zjistím tu velikost zobrazení? Třeba jak je na obrázku síla Fi, vím, že její velikost je dejme tomu 15kN, jak ale zjistím tu velikost v centimetrech, jako jak dlouhá bude ta šipka na papíře? (mám v zadání pouze velikost síly souřadnice jejího počátku a úhel alfa)
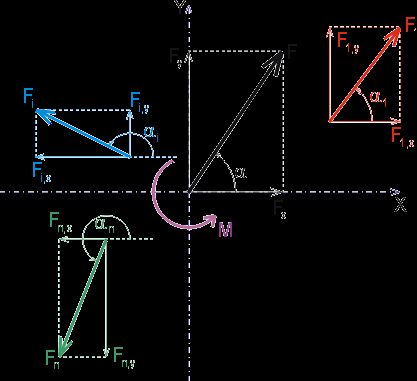
takže to se nijak nevypočítává, to si prostě zvolím? :-o ...a já už si s tím hodinu lámu hlavu! ![]()
Doplníš si dvě síly, vycházející ze společného počátkun na rovnoběžník. Výslednice má koncový bod v protilehlém vrcholu, počáteční v počátku. Výslednice je tedy úhlopříčkou čtyřúhelníku, vycházející z počátku. P0očetně se to dá zpracovat pomocí trigonometrie nebo vektorového počtu.
Obecně vektor je veličina, která má velikost a směr. To je tak zvaný volný vektor a ten múže být kdekoli; já jsem si volný vektor vždycky představoval jako mrak šipek.
U síly ovšem může záležet ne tom, kde působí; třeba síla působící v těžišti jinak volného tělesa bude těloso posouvat, bude-li působit mimo těžiště (přeněji mimo přímku procházející těžištěm, přidá se k tomu otáčivý účinek. Zde mluvíme o vázaném vektoru, a ten údaj navíc, místo, kde působí, je působiště (případně působnice). Pak stejně čtěte předchozí odpověď jojozka. Pokud síly mají působiště v počárku, výslednice ho tam bude mít také, prostě to bude úhlopříčka výše popsaná.
Nebo jak jste to myslel, ten dotaz?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.