Zdravim, vůbec nechápu, jak udělat podle souřadnic bod v prostoru. Chápu ten princip, ale vůbec nevim, jak to narýsovat. Kort když je souřadnice x kladná, y kladná a z najednou záporná. Možná jen nechápu zadání domacího úkolu.
Jaký geometrický útvar vytvářejí všechny body X, jejichž souřadnice x, y, z splňují podmínky:
a) x = 6,
b) y = 8,
c) z = -3,
d) x = 4 a zároveň y = 8,
e) y = -4 a zároveň z = 7,
f) x = 1 a zároveň z = -5.
Nevim jak na klávesnici udělat znaménko "a zároveň", které tam je napsané, každopádně vypadá jako> akorát směřující vzhůru. Budu fakt vděčnej za vysvětlení a postup. Kdyby tam bylo napsané místo těch os ten bod a jeho 3 souřadnice, tak vim. Ale prostě takhle vůbec nevim, co po mě učebnice chce. Díky moc.
2x
Už ze zadání je vidět, že řešením není jediný bod. Máš určit útvar.
a) Jsou to všechny body, které mají Xovou souřadnici =6, takže X=6, Y=cokoliv, Z=cokoliv. Zkus si to představit. Je to rovina kolmá na osu X a tu osu protíná v bodě 6 (tedy přesně [6,0,0]). Opravdu si to představ a bude ti to jasné.
d) Jsou to všechny body, které mají Xovou souřadnici =4 a Yovou souřadnici 8, takže X=4, Y=8, Z=cokoliv. Takže hledáš body [4, 8, cokoliv]. Zkus si to zas představit. V souřadné soustavě vyneseš souřadnici X=4, Y=8 a ... Z libovolnou, takže je to přímka. Přímka rovnoběžná s osou Z procházející (např.) bodem [4, 8, 0]
Snad jsem to nepomotal.
Díky za radu. Zadání už chápu. Ještě jen taková otázka. Když bude teda xová souřadnice 6, y třeba 0 a z taky 0, tak by ten bod měl ležet 6 jednotek do prava od počátku na ose X, je to tak?
Udělal jsem to, jak jsi radil a vyšlo mi tohle. imageshack.us/... Už to asi chápu, ale když všechny ty body spojim, tak mi vyjed takový útvar, který jsem nikdy neviděl. Řekni mi tvůj názor, jestli to mam dobře či ne. Jen dodám, že ty souřadnice, který jsem si měl libovolně zvolit, jsem všechny zvolil jako 0.
Ale ty souřadnice nemám volit (libovolně), ty souřadnice jsou libovolné, prostě jak praví hm, tvoří mnořinu, tu rovinu, tu přímku. Mám pocit, že pokládáš zadání za popis jediného útvaru, ve skutečnosi je to šest různých úloh, které mámo řešit nezávisle na sobě.
Udělal jsem podle těch 6ti zadaných souřadnic 6 bodů. Nenazval jsem je body X, ale A,B,C,D... Doufám, že jsi to co jsi napsal nemyslel tak, že budu dělat kadý bod zvlášť na nové roviny. Myslím to tak, že udělám roviny pí, ný, mí, do nich vyznačím bod A a další body budu dělat znovu pod sebe na nově narýsované roviny? Nevim jak ti to mam vysvětlit.
Jak bylo řečeno, jde o šest nezávislých úloh. Je ti jasné že jde o šest úloh?
Ale třeba řešením té první úlohy není ten bod A, ale celá rovina, bocem A procházející a rovnoběřná s rovinou yz. (Otázka je: Jaký geometrický útvar...
Napíšu a namaluju analogickou úlohu ve dvou dimenzích, pro kterou bude obrázek jasnější:
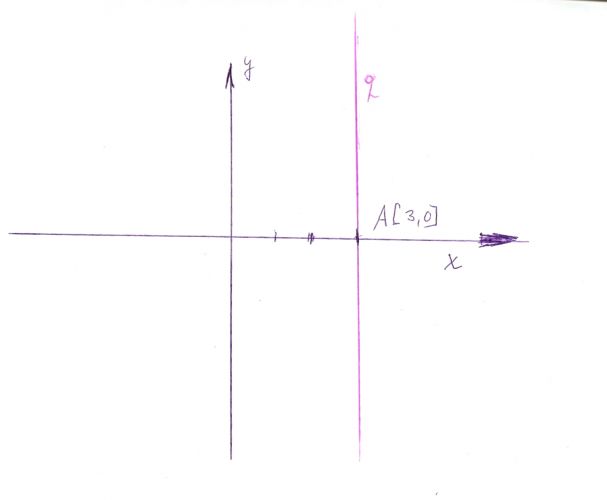
Jaký geometrický útvar vytvoří všechny body x,y, splňující podmínku x = 3
(trochu to odpovídá úloze a) ze zadání).
Nuže, tomuto zadání vyhovuje bod A[3,0], ale nejen on; spolu s ním i třeba bod [3.1], bod [3,π] atd. atd. Hledaný útvar pak je celá přímka q.
Podobně v tvé úloze musíš nakreslit celou rovinu rovnoběžnou s rovinou yz , čili ty další body vyznačíš ne každý v novém obrázku, ale "všechny v tom samém", Jak? Asi takhle: nakreslíš přímky bodem A, rovnoběžné s osami y,z, a ty určují rovinu, která je řešením ůlohy a). Tím jsme s úlohou a) skončili, výkres si uložíme a další úlohu, tedy b), budeme řešit v novém výkresu. ten pak uklidíme a začneme úlohu c§ úplně od začátku, výsledky těchto řešení navzájem nesouvisí a nijak je nespojujeme.
Pokud jsou souřadnice libovolné, tak to znamená, že si můžu zvolit libovolnou souřadnici... Takže vůbec nechápu začátek tvý odpovědi ![]() .
.
Ale ne, to jsi zase zvolil jednu z možností, sice jsi zvolil "všechny souřadnice", ale jen jeden bod. Zadání hledá všechny body, pro které x = 6, a ne jeden jediný, pro který ses rozhodl.
Jenže když se nad tim tak zamyslím, tak těch bodů je na té přímce nekonečně mnoho a všechny můžou splňovat x = 6. Takže asi bude stačit udělat jen přímku kolmou k ose x, v určité vzdálenosti (podle zadání x=6, takže 6 jednotek doprava od počátku) a toť by mělo být vše ne? Podobně jako to máš na tom obrázku nahoře. Jelikož vyznačit úplně všechny body splňující x = 6 je nemožné. Jedině to pak zdůraznit popisem. Ale už jsi mi aspoň trochu otevřel oči. Tomu zadání jsem hold nerozumněl no.
Ano, na Kartagincově obrázku jeho zjednodušené zadání (! vynechal třetí rozměr, tedy osu Z) splňují všechny body přímky q, tedy řešením je celá přímka q (nekonečně mnoho bodů).
Tvé zadání a) pracuje s 3rozměrným prostorem, jeho řešením je celá rovina kolmá na osu X a ta rovina prochází bodem [6, 0, 0]. Tedy Kartagincův obrázek musíš doplnit třetí souřadnicí - osou Z (ta povede normálně průsečíkem os X a Y), jeho původní bod A=[3, 0] musíš začít značit třemi souřadnicemi (když teď pracujeme se třemi rozměry X, Y, Z a ne jen se dvěma X, Y) a navíc má být x=6, takže A=[6, 0, 0]. Tímto bodem hledaná rovina vede. Na papír se to nakreslí nejlépe tak, že z bodem A povedeš ještě přímku (nazvěme ji třeba "r") rovnoběžnou s osou Z, hledaná rovina pak bude zobrazena těmi přímkami "q" a "r".
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.