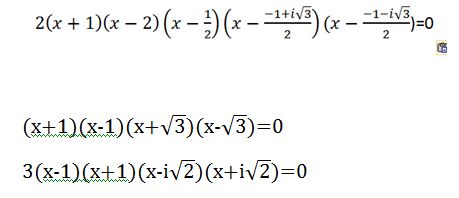Dobrý večer všem, našel by se tu prosím nějaký znalec matiky a látky, u které nemáme nadpis, jen tyhle 3 příklady, které jsme měli udělat ještě v červnu, ale nikdo to neudělal, a přišel nám e-mail, že to máme mít v září vypočítané, že bude opakovací písemka. Ano, škola bohužel začíná, začíná peklo. Byla bych vám více než vděčná za pomoc, netuším, jak na to, máme uhádnout jeden kořen, zbytek dopočítat. Výsledky bych mohla sehnat. Prosím!
0x
Nejsem si jistá tím prvním, ale druhý a třetí bych řešila substitucí, dosadila bych u=x na druhou. Takže u^2 - 4u + 3=0, klasicky vyřešit a kořeny pak dosadit ještě do substituce. Třetí stejně. 
Nooo, tak z hlavy nevím, pardon. Leda si tu substituci představit v hlavě a použít Viettovy vzorce. 
Co to je za debilní požadavek, kořeny povinně jen odhadovat?!
U 2) a 3) na mě fakt čistě náhodou vykouknul kořen 1: 1 - 4 + 3 = 0 a 3 + 3 - 6 = 0. Vlastně x^2 je 1, takže máme hned kořeny 2: x=+1 a x=-1. Víc ale neodhadnu, použil bych už zmíněnou substituci.
U 1) by bylo výhodné, aby se členy se sudými a lichými mocninami navzájem "požraly". To lze tak, že liché budou záporné a sudé kladné, takže x=-1. Pak 2*(-1) - 1 - 4*(-1) - 4 -(-1) + 2 se opravdu = 0. Ale další nevím.
Jen se podivam na druhou rovnici a uz vidim, ze koreny jsou 1 a 3. Pak se to da napsat jako: (x2 - 1) (x2 - 3) = 0
To same s treti rovnici: podelit trema a pak: x4 + x2 - 2 = 0 a hned vidim, ze koreny jsou 1 a -2 a lze to tedy prepsat ve tvaru: (x2 - 1) (x2 + 2) = 0
Jak se na ty koreny prijde? Jestli kvadraticka rovnice ma tvar: x2 + bx + c = 0 a jeji koreny jsou "p" a "q", pak pro ne plati: "pq = c" a "p+q = -b".
V prvnim pripade tedy: b=-4; c=3; p=1; q=3; pq=3=c a p+q=1+3=4=-b
Stejne lze spocitat pro ten posledni priklad.
V zadani se nerika nic o tom, ze je zakazana substituce nebo ze se koreny nemohou pocitat. Neumim si prestavit, ze by bez techto dvou pomucek mohl bezny zak ty priklady spocitat.
Co se tyka prvniho prikladu, u toho se musim trosku zamyslet (zrejme o vhodne substituci).
Vysledek druheho prikladu lze samozrejme jeste dale rozepsat na korenove cinitele tech vyrazu v zavorkach: (x + 1) (x - 1) (x + odm(3) ) (x - odm(3) ) = 0; kde odm(3) je odmocnina ze 3.
Stejne tak ten treti priklad: (x + 1) (x - 1) (x2 + 2) = 0; protoze (x2 + 2) nema zadne koreny v oboru realnych cisel (vyjde, ze x je ±odm(-2) )
Zatim nejlepsi uprava te prvni rovnice, na kterou jsem prisel je tato: (x + 1) (2x4 -3x3 -x2 -3x + 2) = 0
Z toho je videt ten koren x = -1, jak uz odhadl @hm vyse.
Myslim, ze s lepsi upravou budeme muset pockat az na Kartagince, az se rano probudi, nebo doufat v me osviceni :D
Jak konkrétně jsi přišel právě na tuto úpravu, nevímPuvodni rovnici jsem upravil na tvar:
2(x5 + 1) -x(x3 + 1) -4x(x + 1) = 0
Z toho je videt (pokud clovek zna prislusne vzorce), ze kazda zavorka obsahuje (x+1), takze jsem dlouhym delenim zjistil (x5 + 1) : (x + 1) a pak i (x3 + 1) : (x + 1)
(x + 1) jsem tedy vytkl ze vsech clenu a po uprave vyjde to, co jsem psal v predchozim prispevku.
je pak možná (jak někde píšu níže) substitucíNa tu vhodnou substituce se asi jen tak neprijde na miste, ze? Ja na to neprisel
To se musi vycist nekde z tabulek, ne? (Postupy reseni reciprocnich polynomialnich rovnic).Tak ten uvedený postup (je to ten druhý z těch, o nichž jsem psal) využívá symetrie (reciprokosti) uvedené rovnice a podobná úvaha by mohla pomoci i k nalezení substituce. Ona je to teoretická substituce užívaná pro reciproké rovnice. Já na ni sám nepřišel a ani nedovedu říci, jestli bych ji dokázal vymyslet, kdybych ji neznal. Ale když si tak přemýšlím o různých možnostech, napadá mi, že pokus zdůraznit symetrii té bikvadratické rovnice tak, že ji vydělím x², by člověka napadnout mohl a odtud je k substituci už jen krok.
0x
Já si nemůžu pomoci, ale požadavek, že mám kořen uhádnout, bych chápal tak, že si mohu hádáním vypomoci, a ne tak, že nic jiného dělat nesmím.
Jinak se nabízí (zejména u té první rovnice) hledat pro začátek kořeny celočíselné. Pokud rovnice s celočíselnými koeficienty takový kořen má, musí být dělitelem absolutního členu, (proč, to je doufám jasné?), čili začnu tím, že vyzkouším x = 1, x = -1, x = 2,x = -2 a hle, x = -1 a x = 2 jsou kořeny. (Kdybýych takhle žádný kořen nenašel, měl bych smůlu.)
Následně vytknu příslušné kořenové činitele a úloha se mi převede na rovnici třetího stupně; konkrétně to bude
2x^3 +x^2+x-1 = 0
(aspoň doufám, raději si to přepočítejte). Pak bych zkusil ještě kořen tvaru x = 1/y, a když tu rovnici vynásobím y^3, zjistím, že y musí být dělitelem dvojky, tedy y = -2 (to nevyhovuje), nebo y = 2 čili x = 1/2, což je další kořen. Tím mám tři kořeny a zredukují to na kvadratickou rovnici, kde už opravdu nevídím jinou cestu, než použít vzorec (případně doplnit na čtverec, což je ale vlastně jen odvození vzorce).
Jinak ta první rovnice je reciproká rovnice prvního druhu (tj., názorně řečeno, když koeficienty čteme zprava doleva, dostaneme totéž jako při čtení zleva doprava) lichého stupně. Jako taková má kořen x = -1 (což ostatně jsme již zjistili) a tak ji můžeme vydělit kořenovým činitelem (x+1). Vznikne reciproká rovnice prvního druhu čtvrtého stupně, kterou vydělíme x2 (to si můžeme dovolit, protože nula není kořenem) a na vzniklou rovnici použijeme substituci
x +1/x = y.
Po jednoduchých úpravách vyjde kvadratická rovnice pro y. Když její kořeny (dva) dosadíme do té substituce, dostaneme dvě kvadratické rovníce pro x, celkem tedy můžeme očekávat čtyři kořeny, plus tu -1, kterou jsme začali. Jak prosté, milý Watsone .
Více o repciprokých rovnicích třeba na wikipedii
Vůbec nerozumím tomu, co po mně chcete všichni... Já to takhle nepochopím, potřebuji to vidět vypočítané, sama si projít postupy. Nevadí. Ale děkuju všem za snahu, nečekala jsem tolik odpovědí.
No ono je to těřké, napsat to vypočítané, a popravdě nevím, jestli je to ta pravá cesta k pochopení. Ty příklady nejsou na dva řádky a asi to budeš muset zkusit sama, ale chápu, že ten celkový výpočet podle návodů zdše uvedených je dlouhý a je toho moc najednou, Ale zkusím poradit po částech, ale výpočet sem nedám.
Tak začnu tou první rovnicí, když už jsem o tom psal, a uvidíme. Ten druhý postup, přes reciproké rovnice, je dosti složitý a dával jsem ho sem spíš pro úplnost, ale konec konců doporučeno máte zkusit řešení uhádnout. A jak ho uhádnout? Někdy ho skutečně řešitel "vidí", jak píší někteří o těch dalších rovnicích, no ale to chce určitou zkušenost, praxi, představivost. Ale opravdu, co ti brání zkusit tam dosadit x = 1 nebo x = 2. Tak začni tím. No a zjisti, zda některé z těchto dvou čísel je kořenem, když nebude (nebi i když bude), zkus ještě x = -1, nebo x = -2. Pokud tohle nezvládneš, nezvládneš nic, tak tím začni a napiš, k čemu jsi došla, a pak půjdeme dál.
(Já jsem psal něco o té dělitelnosti, ale to vlastně tak úplně nepotřebuješ, to má ten význam, že budeš vědět, že například nemá smysl zkoušet x = 3 a tak dále. Tak na to zatím zapomeň, třeba se k tomu vrátíme později.)
doplněno 25.08.13 17:21:Ještě napiš, co víš o rozkladu na kořenové činitele, jestli víš, co to je a jestli umíš/neumíš kořenový činitel vytknout. Podle toho pak budeme postupovat dál-
Vím sice, co je to rozklad na kořenové činitele, ale stejně tohle mi rpostě nejde. :D Já na to asi kašlu, to je k zbláznení. Učitel se asi zbláznil.
Počkej, ty chceš říci, ýe neumíš vypočítat polynom , tedy dosadit do něj, kupříkladu, x ´-1 a přesvědčit se tak, zda to je či nění kořen?
To snad nemuslíš vážně.
Následně vytknu příslušné kořenové činitele a úloha se mi převede na rovnici třetího stupněJak se prijde na tu kubickou rovnici (krome dlouheho deleni [polynomu], ktere jsem pouzil ja)?
Navic mi nepripada na zaklade zde predlozenych reseni, ze ten prvni priklad by dokazal bezny stredoskolak spocitat. 
0x
Dobrý den, není to nic těžkého. Ta první rovnice, jež je 5. stupně, tak se musí zkusmo uhodnout kořen, jelikož to jsou školometské příklady, lze předpokládat, že bude celočíselný. Takže zkusit náhodně dosazovat +1, -1 a pod. Bude vidět, že kořen, náhodně zvolený -1 vychází. Tudíž celý polynom 5. stupně vydělíme polynomem x- (-1) a dostaneme bez zbytku (což je kontrola) polynom 4. stupně. Takže se rovnice pátého stupně rozpadne na součin dvou výrazů a jejich součin je roven nule. To je tehdy, když jeden i druhý je roven nule. Ten druhý, to již víme, jelikož z toho jsme vycházeli. Takž zbývá řešit rovnici čtvrtého stupně. To lze dokonce i exaktně, ale řešení vychází z exaktmího řesšení rovnice třetího stupně a obojí není vůbec nijak jednoduché. Lze také Čebyševovou metodou přes trigonometrické funkce, také to není jednoduché. Takže lze zkusit trik, jelikž to je školometský příklad, tak zda rovnice není tzv. reciproká. To jde tehdy, když zde máme tedy čtyři členy a rovnici vydělíme výrazem x^2. Pak vhdně přeskupíme a ponecháme absolutní člen. A opravdu, je tomu tak. Takže lze pak položit substituci a dostaneme již redukovaou rovnici druhého stupně, kterou dořešíme a zpětně dosadíme a dostaneme opět rovnice drruhého stupně a z toho čtyři ko¨řeny a ten úplně první k tomu, celkem 5. Takže níže je výsledek na papíře. Tedy bude, až bude lze vložit obrázek, což zatím nelze.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.