Nejste přihlášen/a.
Dobrý den, mám před sebou matematiku, konkrétně stereometrie, příklady. Výpočky objemu, obsahů atd.
Vše by bylo v pořádku, kdybych jen dosazoval do vzorců, mám tu ale dost těžké úkoly.
1: Objem kvádru ABCDEFGH se čtvercovou podstavou je 64 cm(3). Odchylka tělesové úhlopříčky AG od roviny podstavy je 45°. Vypočítejte jeho povrch.
2: Vypočítejte délku podstavné hrany pravidelného pětibokého hranolu, jehož výška je stejná jako délka podstavné hrany. Objem hranolu = 100cm (3)
3: Pravidelný komolý pětiboký jehlan má podstavné hrany délek 6cm a 4cm. Boční hrana svírá s rovinou podstavy úhel 60°. Vypočítejte objem a povrch komolého jehlanu.
4: Rotací pravoúhlého trojúhelníku ABC kolem odvěsny BC znikne rotační kužel, rotací téhož pravoúhlého trojúhelníku ABC kolem odvěsny AC vznikne jiný rotační kužel. Vypočítejte poměr objemů těchto dvou kuželů.
5: Nálevka má tvar rovnostraného kužele. Vypočítejte obsah plochy smáčené vodou v případě, že do nálevky nalijete 3 litry vody.
6: Jaká je přibližně délka vlny, která je namotána na kloubku tvaru koule o poloměru 8cm, je-li průměr vlny 1mm?
Všem moc děkují za případné odpovědí píšeme z toho závěrečnou písemnou práci a já netuším, nemám váźně ani ponětí jak na to...
1x
Já nechápu co to dnes chodí za trdla do školy. Vyhulené mozky marjánkou, budiž, ale ani trochu vlastní snahy. Při tom tak jednoduché příklady. Třeba ten první. Každý snad pochopí, že ten kvádr je vlastně krychle o hraně 4 cm, takže povrch je 96 cm²
doplněno 18.06.13 00:01:No sorry trochu jsem se sek, hlavně když se člověk včas opraví. V zadání je tělová uhlopří čka, takže to bude otrochu více. Hledám kus papíru.
doplněno 18.06.13 00:56:Spíš pořádnou kalkulačku a je to 97.236 cm²
doplněno 18.06.13 03:26:2/ 3.87 cm
1x
Tazatel již asi počítá, že se neozývá.
3/ Vzoreček na obsah pětiúhelníka máme, takže by neměl být problém vypočíst objem komolého jehlanu jako rozdíl objemu dvou jehlanů o různých základnách a výškách, když výška je V=Ro * tg(60) teda ten tg ve stupních
doplněno 18.06.13 11:44:A povrch vypočíst bude asi nejlepší použít Heronův vzorec na výpočet plochy trojúhelníku.
doplněno 18.06.13 11:57:Koukám, že tady máme s kartagincem vzájemnou předobědovou rozcvičku. Tak aspoň ten Heronův vzorec.
Ale ten poslední příklad výpočtově snad nejlehčí, ale matematicky pěkně přitažený za vlasy.
Na povrch jsem zapoměl. Ale Heronův vzorec se mi možná nzdá nejvhodnější (i když by seurčitě nějak aplikovat dal).. Bošní stěny jsou tvořeny lichoběčníky (pěti), tak bych se raději pokusil spočítat jich výšku (strana bude (Ro = ro)/cos 60°, nebo ji lze vypočíst přes Pythagora) Připomínám, že Ro (resp. ro) je poloměr kružnice opsané dolní (resp. hurní) základně.
doplněno 18.06.13 12:21: Jirbar: občas se míjíme ![]() , ale stejně bych byl rád, kdyby se tazatel ozval, zda mu to pomohlo.
, ale stejně bych byl rád, kdyby se tazatel ozval, zda mu to pomohlo.
Ten Heronův vzorec jsem měl na mysli rozdíl ploch obdobně jako objem. A co se týče tazatele nerad bych mu křivdil. Třeba teď právě úporně počítá. Víc mně vadí, že si dovolí "zadat" příklady aniž by aspoň naznačil svoji vlastní minimální snahu.
To je pravda. Znamenalo by to zase spočítat délku tělesové hrany. Já si původně představoval rozklad těch stěnových lichoběžníků na trojúhelníky, tam by toho počítání bylo neúrekom.
A co se týče tazatele, já na něj nepospíchám, někdy bych rád věděl, co on na to. Tu snahu projevit mohl, no ale říkal, že dosazování do vzorců umí, i to je něco.
0x
Ad 1. Číselný výsledek napsal Jirbar, nekontroloval jsem ho, jistě bude dobře. Naťuknu postup:
Čtvercová základna má sranu AB a úhlopříčku AC. Oznaším-l délku stranu a, tak délka (stěnové) úhlopříčky AC se spočte snadno ze vzorečku (a krát odmocnina ze dvou).
Trojúhelník ACG je rovnoramenný, takže délka hrany CG (výška hranol) je stejná jako délka AC.
No a taď už je to dosazování do vzorečků: a vybočtu ze známého objemu a dosadím do povrchu.
Ad2: Objem hranolu je základna krát výška, jde tedy o to, umět spočítat obsah základny. Na to je vzorec (viz obrázek), ale početně jednodušší je počítat to pomocí středového úhlu a goniometrických funkcí (viz například forum.matweb.cz/...; to není hotový vzoreček, ale ten si jistě najdete).
dále po kafi.
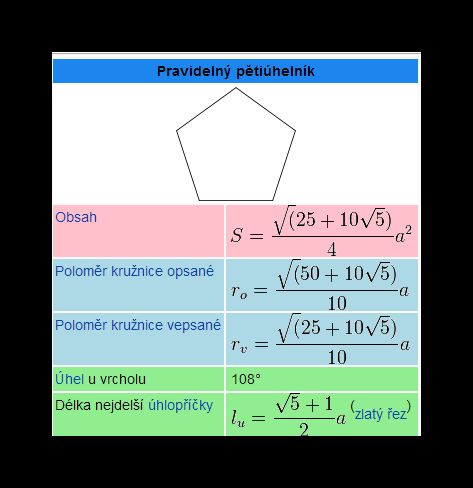
Ad 3: Vzoreček pro výpočet objemu jehlanu (1/3 základna * výška) znáte, pro komolý jehlan byster to měl taky vědět (lze spočítat jako rozdíl "nekomolého jehlanu"a "uříznuté špičky", nebo použít přímo výsledný vzorec, viz třeba aristoteles.cz/... nebo cs.wikipedia.org/... v každém případě potřebujete znát obsahy základen -zde pěttiúhelníků, což už umíme. a výšku komolého jehlanu, kterou spočteme pomocí goniometrických funkcí takto: spočteme poloměry kružnic opsaných těmto pětiúhelníkům (vzoreček výše) a jejich rozdíl násobíme tangentou šedesáti stupňů.
ad 4. Ta odvěsna, kolem které rotujeme, bude představovat výšku kužele a te druhá poloměr základny. Objem je úměrný výšce a druhé mocnině poloměru zákaldny (snadno zjistíte ze vzorečku pro objem, z něhož spočtete i konstantu úmerosi) a poměr obsahů je tedy roven poměru těch odvěsen.
doplněno 18.06.13 11:29:Ad pět: Vzorec pro objem kužele v závislosti na výšce a poloměru základny (který je zde rovenvýšse) známe. Znéme též objem vody, spočteme výšku a pak už je to vzorec pro povrvh (vzorce umíte.)
Ad 6. Znáte objem koule, což je tím pádem i objem vlny, vlna je vlastně válec (rotační) o průměru základny 1 mm a o výšce rovné délce vlny, a tu hledáme.
doplněno 18.06.13 23:10:Ke čtyřce: ve snaze po stručnosti jsem se možná nevyjádřil dost jasně. Poměr obsahů rovná se poměru odvěsen, kolem kterých trojúhelník nerotuje. Nebo ještě jinak: obsah kužele, který vznikne rotací pravoúhlého trojúhelníku ABC kolem odvěsny BC , označím O1, ten druhý O2. Pak je O1:O2 =|AB|:|BC|
No, tak jsem nad tím včera proseděl celý den místo opalování a pobíhání venku, pár propocených hodin nad popsaným sešitem a voila, za dva z písemky ![]()
Ve skutečnosti ne, nejsem "prohulený mozek" ani nic takového, jen paní učitelka na nás doopravdy kašle, neumí zaujmout, ani nic podobného. Ona jinak prostorová matematika vcelku zajímavá je.
Ale to jdu od tématu.
Všechny úlohy jsem víceméně vypočítat s Vaší pomocí dokázal. S čím byl obrovský problém, který i teď přetrvává je poslední úloha. Holt na ni nejspíš nemám mozek, nebo to je tím horkem, prostě si to nedokážu představit. Heronův vzorec jsme teda ještě neprobírali, nebo o něm alespoň nevím.
Každopádně moc děkují za Váš čas a snahu, hodně mi to pomohlo ![]()
Děkuji za zprávu a blahopřeji k dvojce.
Jinak, Heronův vzorec je vzorec pro výpočet obsahu trojúhelníka, znáte li jeho strany a,b,c: označíte s = ½(a+b+c) poloviční obvod, spočítáte s(s-a)(s-b)(s-c) a odmocníte. V zásadě není tak nutné ho znát, stačí vědět, že něco takového existuje a pak už si to najdene (třeba cs.wikipedia.org/...
A ten poslední příklad jistě taky rozebereme. O který vám jde? Poslední je s tím klubkem vlny, ale podle toho, že v souvislosti s ním mluvíte o Heronovu vzorci, se mi zdá, že byste mohl mít na mysli ten komolý pětiboký jehlan. Tak napište a podíváme se na to.
Podle mne je právě ten poslední příklad nejjednodušší. Podstata je vypočítat výšku válce o průměru 1mm který má stejný objem jako koule o průměru 160mm. Ikdyž z praktického hlediska je to blbost. Ostatní příklady, hlavně ty s definovaným pětiúhelníkem jsou horší. A doufám, že jsme se aspoň sešli ve výsledku těch dvou příkladů.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.