Nejste přihlášen/a.
Potřeboval bych poradit s úkolem do matematiky:
Máme papír Ax (normalizovaný např. A4,A3...)
Když s papíru vyřízneme 5-ti cípou hvězdu (co nejětší) kolik procent bude tvořit hvězda a kolik procent bude tvořit ten zbytek?
Potřebuji vytvořit vzoreček za který když dosadím velikost papíru, tak mě výjde kolik procent bude tvořit hvězda a kolik ten zbytek (okolo hvězdy).
2x
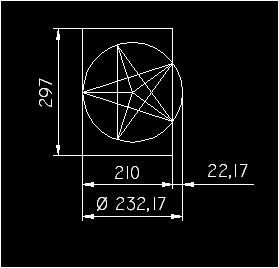
formát A4 má rozměry 297 x 210
formát A3 má rozměry 420 x 297
A hlavně, na formátu nesejde, protože každý další formát je vždycky 2x větší, než ten předchozí.
Poměr ploch hvězda/papír se nemění.
Chce to splašit někde v tabulkách vzorec na výpočet plochy pěticípé hvězdy. Ten vám nikdo z hlavy neřekne.
Tady máte obrázek hvězdy na formátu A4, vymyslete vzoreček, který plochu hvězdy dělí plochou formátu a výsledek vynásobí 100.
Výsledek vyjde v procentech.
doplněno 13.06.13 17:14:no tak nejjednodušší metoda jak zjistit plochu není vystřihnout hvězdu z papíru a v lékárně zvážit jak jsem si právě přečetl, ale narýsovat si ji v ACADu a potom použít funkci Area.
plocha pěticípé hvězdy vepsané do formátu A4 = 15127,4170 mm2
to je 24,2543161 % z plochy formátu A4. ![]()
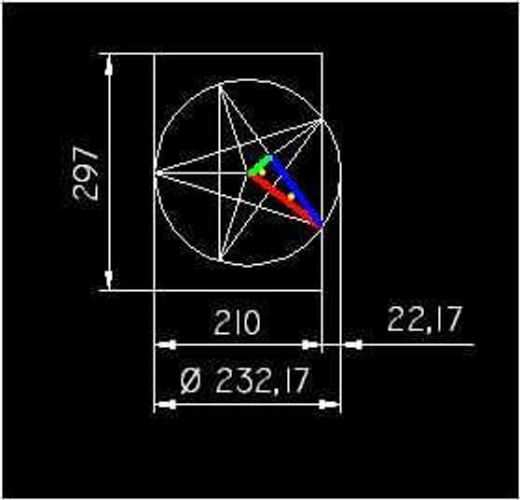
Zacal bych asi hvezdou vepsanou do jednotkoveho kruhu, takze cervenou znas, zlute uhly znas, modrou si dokazes spocitat (kosinova veta s trojuhleniku k tomu vrcholu nahore, tedy jedna strana je dvojnasek modre a zbyle 2 strany jsou cervene), pak uz rovnou spocitat obsah toho barevneho trojuhleniku, nebo dopocitat zelenou a pak vysku a pak obsah.
Nakonec jen spravne nacpes ten jednotkovy kruh na ten obdelnik (asi pres to, jaka je vzdalenost od jednoho vrcholu k primce mezi dvema protejsimi vrcholy u hvezdy v jednotkove kruznici) a melo by jit.
0x
Pro začátek bych si uvědomil, že všechny normalizované archy (A1, A2. A3... ale i B1, C1 atd) jsou si podobny (proč? připomeňte si charakteristiku normalizovaných formátů) a tudíž to hledané procento na konkrétní volbě velikosti (tedy v rámci řady Ax) nezáleží (proč?).
doplněno 12.06.13 16:01:Figurek nakreslil pěký obrázek a navrhl dobrý plán, je fakt, že jeho realizace není nejjednodušší (to je ovšem v podstatě věci, není to chyba plánu). Něco o pětiúhelníku najdete třeba na cs.wikipedia.org/... kde je mj. obsah konvexního pětiúhelníka, ale vidíte, že ani ten není nejjednodušší a vypočítat obsah pentagramu (té hvězdy) představuje další komplikaci. Můžete zkusit od pentagonu odečíst obsah těch vystřihnutých kousků, nebo naopak k obsahu vnitřního pětiúhelníku (jehož strany spočtete pomocí poměru zlatého řezu, to tam taky je) připočítat obsah "cípů", ale jednoduché to není. A to ani nemluvím o tom, že vzorečky ve Wiki napsané vycházejí z délky strany, kterou musíte taky znát. Budete-li znát poloměr kružnice opsané, stranu spočítáte, ale ta kružnice opsaná je další problém, znáte jenom stranu papíru (ve figurkově nákresu je to těch 210 mm,) ale poloměr kružnice opsané je větší o výšku té kruhové úseče (u figurka o těch 22,17 mm). Opravdu vám učitel zadal tak složitý úkol? Nebo mu bude stačit plochu hvězdy změřit (či vypočítat z údajů, které na ní naměříte) a jde o tu závislost na formátu, (tedy na tom x z označení Ax)? Pro jakou úroveň to je?
Ještě drobnou, nepodstatnou připomínku: v řadě A je každý další formát 2x větší než předchozí plošně, lineární zvětšení (tedy poměr odpovídajících stran) je v poměru odmocnina ze dvou.
doplněno 12.06.13 16:05:Ono když si vypomůžeme goniometrickými funkcemi, zvládneme to spíš, ale má otázka na úroveň žáků (která třída? jaká škola?) zůstává.
0x
Jak uz ti vysvetlil Kartaginec, na vlastni velikosti papiru nezalezi, protoze vsechny maji stejne pomery stran a tak ten pomer hvezda/zbytek pro ne bude pro vsechny stejny.
0x
Podle mne je sem to zadani chybne opsano/ interpretovano, dost mozna, ze uz bylo chybne pochopeno ve skole.
Jak jiz na zacatku pise Kartaginec, pomer - procento bude vzdy na podobnem formatu stejne. Ucitel toto zcela jiste vi a neptal by se tedy po procentu pri zadani libovolne velikosti normalizovaneho formatu.![]() Aby to melo smysl, tak otazka musi znit jinak.
Aby to melo smysl, tak otazka musi znit jinak.
Děkuji za odpovědi. Jsem ve druhém ročníku na silnoproudu, na učebním oboru (máme to jako dodatečný úkol). Goniometrické funkce umím. Potřeboval bych to nějak pomoct spočítat protože já pořád nevím jak na to.
Tak především jsme se dohodlí, že všechny archy formátu Ax mají strany a, a*sqrt 2 (sqrt nísto druhá odmocnina). a že díky tomuto poměru nezáleží na tom, pro který konkrétně formát to počítáme a dokonce ani to nemusí být některý z techto formátů. stačí, aby jeho strany byly v tomto poměru. Souhlasíte s tím, nebo k tomu potřebujete ještě něco vysvětlit?
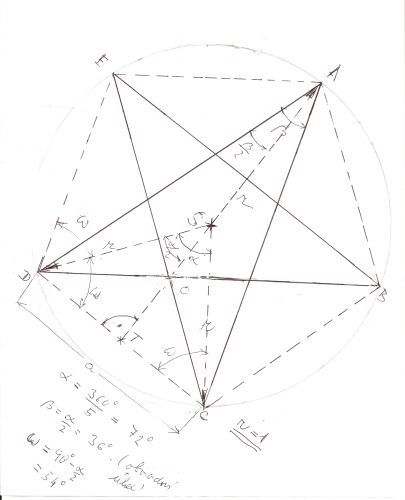
Pokud souhlasíte, ulehčíme si práci: místo toho, abychom do normalizovaného archu vepisovali pentagram, začneme pětiúhelníkem (konvexním), vepsaným do jednotkové kružnice, a pentagram vepíšeme do něj. Spočítat plochu nebude zase tak obtížné (s pomocí goniometrických funkcí) a následné opsání obdélníku už by měla být brnkačka. Zkuste si ten pětiúhelník nakreslit, zapřemýšlejte, jak spočítáte jednotlivé úhly a co s tím dál. Já teď jdu venčit psy, tak sem zatím napište, jestli toto vám k něčemu je anebo zda byste potřeboval nějakou další radu, a já se sem později podívám a ozvu se.
Dobře, ohledně tech papíru to chápu. Ale ohledně té hvězdy pořád nevím uplně přesně jak na to ![]() . Poradíte mi prosím.
. Poradíte mi prosím.
Snad pomůže obrázek.Na něm zjistíte úhly a délky, které budete potřebovat. A pak je můžete využít k dalším výpočtům. Možná i podle Lukeho, i když trochu potíž vidím v tom, jak spočítat to, co se překrývá, já bych spíš spočítal obsah trojúhelníku DSC jako ½ r² sin α , a násobil pěti. Od toho bych odečetl desetinásobek obsahu trojúhelníku ODT , k jehož výpočtu použijete úhel γ = ODT (ten jsem tam nezakreslil, už by toho bylo moc, ale jistě ho spočtete) a strany |DT|= r cos Ω , |OT| = |DT| tan γ a yak dále a tak dále. Záver podle Luka.
Možná i podle Lukeho, i když trochu potíž vidím v tom, jak spočítat to, co se překrývá
Co se prekryva, je ten pravidelny petiuhelnik v centru te hvezdy. To nemuze byt zase takt ezke spocitat jeho obsah.
Ten trik s vypoctem pred trojuhelnik DSC je moc zajimavy. Takhle jsem o tom vubec nepremyslel.
Je pravda, že to není velká potíž, spíš mně osobně to přišlo trochu komplikovanější, prostě jsem navrhoval to, co napadlo mne, ale jediná možnost to není, ta vaše je rozhodně možná. V podstatě vyžaduje výpočet obsahu trojúhelníku DSO, což lze podobně, jako ten DSC, jen musím znát vzdálenost |SO|= |ST| - |OT|, a následně taky stranu vnitřního pětiúhelníku, což také jde spočítat, a to různými způsoby. Ono jakmile se začneme bavit o tom, co je jednodušší, nevyhneme se subjektivnímu pohledu.
0x
Nevíme, jak přesný má být výsledek. Kdyby na celá procenta, tedy setiny, tak by stačil ůplný primitivismus-přesně to narýsovat na čtvrtku A 4, hvězdu přesně vystřihnout, a v lékárně si nechat zvážit váhu hvězdy a celé čtvrtky. Z toho by se vzorec snadno sestavil=kolik procent je váha hvězdy, kolik procent je do celého formátu. Záleží, jaká přesnost výpočtu je požadována.
Nemohl. Ale zeptám se: jaký vzorec konkrétně chcete? Výsledkem bude číslo, to číslo vám napsal figurek (24,2543161 %), já to sice nekontroloval, ale nemám nejmenší důvod o něm pochybovat. Chete-li vzorec závislosti na formátu, tato závislost je konstantí, výsledkem bude toto číslo pro každý formát řady A (a taky řady B i řady C, ale to jste říkal, že chápete (nebo jsem vás špatně pochopil?) Pokud vám tohle nestačí, musíte obsah hvězdy a obsah papíru spočítat a následně spočítat to procento, jak, napsal explicitně figurek.. To jde samozřejmě různě, jeden až dva návody jste dostal. V kterém bodě je problém?
doplněno 15.06.13 11:08:Zkuste aspoň začít. Nebudu za vás vykonávat mechanickou práci, a myslím, že ani nikdo jiný zde.
0x
Každý na matiku není, o to víc pak záleží na učitelovi, na jeho kvalitě. Já věřím citátu, že "dobrý učitel to naučí každého" Chcete-li vzorec, musíte tu hvězdu mít zadanou, konkretizovanou. Npříklad půměrem opsané kružnice-a to je v našem případě šířka formátu. Stačí?.
Tak ono zas tak úplně jednoduché to není, na obrázku figurka je docela jasně vidět, že poloměr kružnice opsané bude větší než šířka papíru, proto píšu, aby tazartel napsal, co konkrétně neumí. O tom se rád pobavím, ale nehodlám dosazovat do goniometrických funkcí a tak podobně. A, last but not least, opravdu bych rád četl, jaký konkrétně vzorec v posledním dotazu tavi poptává. Chce znát vzorec na výpočet obsahu hvězdy v závislosti na poloměru opsané kružnice, vzorec na výpočet procentního poměru na volbě formátu z dané řady, nebo možná vzorec pro vztah mezi šířkou papíru a poloměrem kružnice opsané... možností je hafo
Já si s tím právě rady moc nevím. Popsal jsem už snad tuny papíru... No potřeboval by jsem vzorec takový, za který když dosadím formát papíru (např. A4, A5,A6,..) tak dostanu kolik procent výjde hvězda a kolik to výjde okolo.
No ale ten máte, vyjde vždy totéž, to už jsme vám napsali mockrát a figureg dokonce napsal kolik (i když si nejsem jist, jestli učitele uspokojí číslo bez odvození, ale odpověď na vaši otázku to je). Takže se zdá, že není pravda, že tomu s tím papírem rozumíte. Tak ještě jednou:
Poměr stran papíru formátu řady A je vždy 1:sqrt 2, tedy všechny tyto formáty jsou si podobné.
(Formát A3 například dostaneme z formátu A4 tak, že všechny odpovídající úsečky (strany papíru, a pokud na něm máte něco nakresleno, třeba tu hvězdu, tak i strany té hvězdy atd.) vynásobíte odmocninou ze dvou. Všechny plošné obsahy se pak násobí dvěma. To znamená, že když do formátu A4 nakreslíte co největší hvězdu s obsahem O, a vše zvětšíte na formát A3, tak se i ta hvězda zvětší a díky podobnosti bude zase největší možná, obsah bude mít 2O. Obsah papíru formátu A3 bude rovněž dvojnásobný než obsah formátu A4. Tahle řada je konstruovaná tak, že obsah A0 je 1 m², obsah A1 tedy 0,5 m² atd., A3 má obsah 1/8 m², A4 je 1/16 m², tedy A3 má obsah dvojnásobný než A4 Teď pro zjednodušení označím jako A4 nejen arch, ale i jeho obsah, a podobně pro A3. Takže A3 = 2A4.
Výpočet procent (viz figurek): u formátu A4 zabírá maximální hvězda (O/A4)*100 %
u A3: (2O/A3)*100 % = (2O/2A4)*100 % = (O/A4)*100 %, tedy přesně totéž.
To okolo dopočítáte do sta procent.
- Popis konstrukce kružnice opsané a vepsané
- Těžký přiklad
- Kružnice vepsaná
- Thaletova kružnice?
- Rovnoramenný lichoběžník+kružnice opsaná
- Zajímavé úlohy
- Kružnice opsaná poloměr
- Opsaná kružnice u trojúh. nelze narýsovat?
- Výpočet obvodu kosočtverce
- Konstrukční úloha
- Plášt rotačního válce
- Délka strany čtverce
- Kružnice vepsaná, opsaná osmiúhelníku
- Logaritmus definiční obor
- Příklady - vektory
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.