Nejste přihlášen/a.
Zdravím, zrovna řeším s dcerkou to co probírají v matematice a narazili jsme na pojem "osa soměrnosti". Ta je tedy jasná, dělí tvar na dvě zrdcadlové půlky.
Moje otazka je taková: Jak se jmenuje osa, která dělí tvar na dvě identické půlky. Přesněji, že tvar bude stejný, ale třeba jinak otočený ( logicky i poloviční původní velikosti)
Takže osa soměrnosti obdelníku může být dvojí ( jsou dvě ) ale tu osu kterou myslím já ta ma milion možmností, jen musí projít středem souměrností, přesněji bodem, kde se uhlopříčky setkají uprostřed tvaru.
Jak se tedy ta osa jmenuje?
doplněno 30.05.13 15:57:obrazek
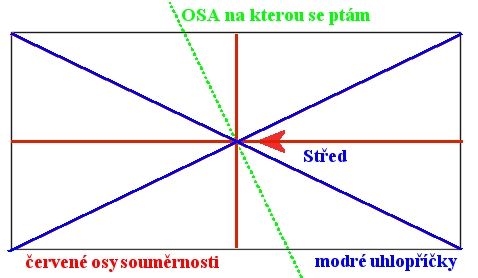
no kdysi jsme tomu říkali, nakresleme osu, jež vytvoří dvě symetrické části. .. takže jmeno nedostala .. tím líp ... a dík, posílam bodíka
doplněno 30.05.13 17:44:@dzordz
Datum: dnes 17:16
Předmět: RE (5x): Jak se jmenuje osa?
... , ale kdžybyste mi zatím nějak srozumitelně vysvětlil, oč vám jde, můžeme se o tom pobavit později.
Jistě pane profesore
"Ano pouze to rozdělím na dvě části, ale u obdélníku, jsou ty části vzdy shodné, stejně jako u kruhu, nebo čtverce..."
Snažil jsem se poukázat na to, že toto vyplývá z vlastností středu souměrnosti ![]() Jakákoli přímka, která jím prochází, tohle způsobí.
Jakákoli přímka, která jím prochází, tohle způsobí.
Přímka prochází středem -> rozděluje útvar tak, jak popisujete.
Dokonce naopak, pokud naleznete dvě (a více) různé takové přímky, jejich průsečíkem bude střed souměrnosti. Žádné jiné takové neexistují. Vše je to odvozeno od souměrnosti podle středu. (a jak píšou ostatní, ty přímky tedy zřejmě speciální název nemají)
0x
To se vám jen zdá, že to rozdělí obdélník na dvě identické půlky. Ve skutečnosti ho rozdělí na dvě části. To otočení z jedné strany na druhou, aby na sebe pasovaly, se provede právě kolem středu souměrnosti. Bez znalosti středu to jsou prostě dvě části.
doplněno 30.05.13 17:36:No že tahle "osa" prochází středem, je hezké. Takže střed leží na ose. Ale kde přesně? Přesně tam, kolem čeho to musíte otočit, aby se to krylo. Takže je tam ta "osa" vlastně úplně zbytečná, že, protože stačí střed. Naopak "osa" bez přesného středu (tj bez té krátké značky-čárky na dlouhé přímce) vám nic neřekne, protože to podle ní rozdělíte pouze na ty dvě části.
Ale vycházíme ze skutečnosti, že znám přesný střed. Někdy mám pocit, že mluvím arabsky.
Takže vystřihnu z papíru obdelník. Rozsřihnu ho na dvě dokonale stejné pulky. Jak se jmenuje osa, po které jsem stříhal?
Možná je to jen "osa"tím, že je přesně v pulce. Kdysi to byla osa, kdysi jsme názvy jako osa souměrnosti neměli, a bylo jasné co hledáme. Dnes se tomu dávají ruzně dementní nazvy.
Kdysi jsme jen nakteslili bud osu, která rozdělí obdélník ba kde shodné poloviny, nebo na zrdcadlově stejné poloviny. Dnes je to osa souměrnosti a osa .. ( kdoví jak)
P.s. Figirek : ze života, osa nemusí procházet středem : viz auto, kde je Hypoidní osa
doplněno 30.05.13 16:12:Figurek : karlova univerzita říká, že osová přímka je: cituji
Shodnými útvary v rovině rozumíme takové dva rovinné obrazce, které se po posunutí na sebe navzájem kryjí.
viz tento odkaz. it.pedf.cuni.cz/...
opravdu si myslíte, že si to jen myslím?
Pokud nevíte odpověď neodpovídejte. "Chytrých"mám kolem sebe desídky. Moudrých poskromnu.
Takže, dle Karlovy univerzity, což Figurek popírá, je osa souměrnosti ta, co vytvoří zrdcadlový obraz.
Moje otázka je, jak se jmenuje přímka, procházející středem, která dělí obraz ( tvar ) na dvě stejné poloviny.
Musím Figurka potvpořit. Vy poněkud matete dohromady pojmy shodnost, symetrie a posunutí. Tak si to přeberte, čtěte i o kousek dále, kde se dočtete
Osově souměrný útvar se dá rozdělit přímkou na dvě shodné části, pro které platí: Když překlopíme jednu část podle této přímky, kryje se přesně s druhou částí.
a tam je i napsáno, že tato přímka je osa souměrnosti. A teď mi najděte, kde tohle Figurek popírá, a pak můžete začít urážet. A jinak, možná to pro vás bude překvapení, ale to, co se píše v tom vačšem odkaze, je blbě nebo přinejmenším nepřesně: v něm je slovo "posunutí" použito ve volném zmyslu běžné řeči, ale v matematice to má naprosto přesný, mnohem užší smysl.
definice, kterou se děti dnes učí ve škole zní : osou souměrnosti, dostaneme přesně zrdcadlový odraz. Z toho vycházím, že asi mají učebnice ( a nové nazvy) asi větší váhu, než někdo kdo píše, že to tak není.
část kterou jsem z dokumentu kopíroval, je ta, na kterou se ptám, tedy aby vznikly dva identické tvary. Tedy něco musí existovat. Třeba i kdyby se to nijak nejmenovalo.
Osově souměrný útvar se dá rozdělit přímkou na dvě shodné části, pro které platí: Když překlopíme jednu část podle této přímky, kryje se přesně s druhou částí.
čímž se potvrzuje, že jde o zrdcadlovou část ( osovou souměrnost), a ne pootočení, na kterou se ptám já.
takže odpověd´, že přímka která dělí něco na dvě pulky není osou, je nesmyslná.
Autor: figurek®
Datum: dnes 14:59
nijak se nejmenuje. Taková přímka není osa.
Vy jste se ptal na tu zelenou přímku, ta se opravdu nijak nejmenuje. Jinak, přímka, která dělí něco na dvě půlky, pravda, může být osou, ale jen náhodou, ne z toho titulu, že neco dělí na dvě půlky.
A začátek této vaší reakce jaksi s debatou nesouvisí, já teď nemám čas to studovat a rozebírat, neb odjíždím, ale kdžybyste mi zatím nějak srozumitelně vysvětlil, oč vám jde, můžeme se o tom pobavit později.
0x
Tak teď k těm výše zmíněným pojmům:
Posunutí je takové zobrazení, kdy máme dán směr a velikost posunutí a každý bod v tomto směru (každý ve stejném) posuneme o tuto velikost (vždy o tutéž).(Pro doplnění: takové zobrazení neponechá na místě žídný bod, nemá invariantní body; výjimkou je samozřejmě posunutí o nulovou vzdálenost, čili totožnost, identita.)
Otočení je zoprazení, kdy máme dán pevný bod S, zvaný střed otočení, a každý bod P kolem tohoto bodu otočíme do bodu P‛ o pevný úhel; berme ho nenulový, přesněji mezi nolou a 360° (jinak máme zase identitu.) Ještě jinak vzdálenost |SP| je rovna vzdálenosti|SP‛| a úhel PSP‛ je pevný (úhel otočení). Toto zobrazení (samozřejmě pokud úhel otočení není roven např. 360 stupňů) má jediný invariant S.
Středová souměrnost je dána bodem S, zvaným (tentokrát) střed souměrnosti, a obraz bodu P bude symentricky podle S na opačné straně (|SP| = |SP‛| a polopřímky SP, SP‛ jsou opačné). (Jediný invariantní bod je zde střed souměrnosti, ale jsou zde ještě invariantí přímky, které se zobrazí samy na sebe jako celek, ale nikoli bod po bodu), jsou to právě všechny přímky, procházející středem symetrie. S pojmem "středová osuměrnost" není spojen žádný pojem osy čehoholi.
Osová souměrnost je zobrazení, které je dáno přímkou zvanou osa souměrnosti a vzniká tak, že obraz vznikne zrcadlovým překlopením podle této osy (nepřímá shodnost, zrcadlení). Invariantí (pevné) body tohoto zobrazení tvoří osu souměrnosti , invariantní přímky (invariantní jako celek, ne bod po bodu) jsou všechny přímky kolmé na osu souměrnosti. Jinak s osovou souměrností není spojen středu čehokoli; váš úvodní obrázek je v tomto ohlledu poněkud zavádějící, jak vysvětlím v dalším.
Takže jediná "osa", se kterou se tady potkáme, je osa souměrnosti. V matematice se vyskytují ještě další "osy" : osa úhlu, osa úsečky (což jsou vlastně osy souměrností), osa souřadná (což už je úplně jiný pojem), ale vždy je to "osa s přívlastkem". Žádnou osu jako takovou, osu "an sich", neznám. Pravda, pokud se zabýváte problematikou shodnosti a symetrie, tak jiné než osa souměrnosti nepřichází v úvahu a tak v zájmu stručnosti mohu tu "symetrii" vynechat, ale zůstává tam přítomna implicitně.
Tyto názvy jsou zavedeny již dávno žádné "nové názvy, které mají větší platnost než (než co?) to nejsou, maximálně se může lišit forma popisu, ale musí popisovat totéž.
To by tedy byly pojmy a v dalším doplnění se vrátím k původní otázce.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.