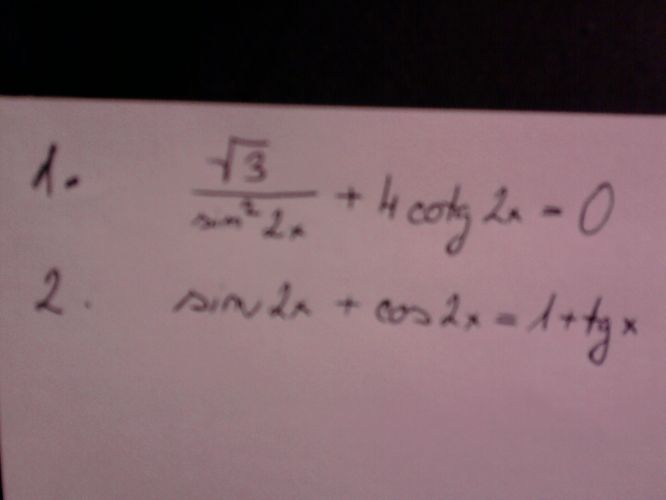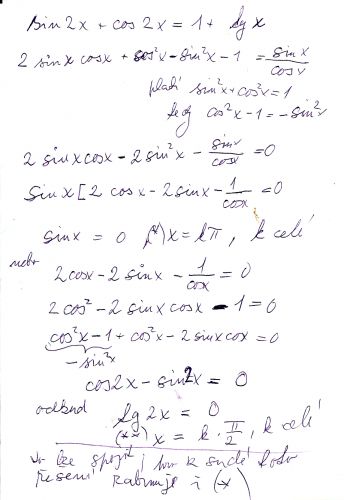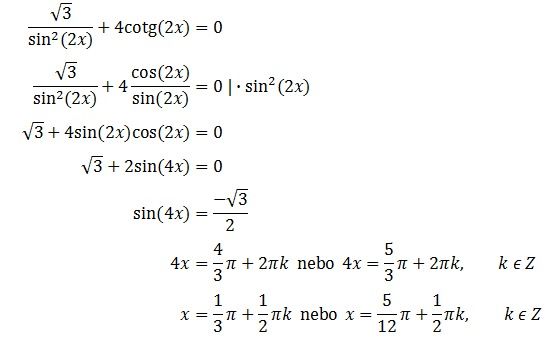Ahoj, mohl by mi někdo prosím pomoc se 2 rovnicemi?...nevím jak je vypočítat, protože ta 1. by se měla počítat pomocí substituce a ta 2. vytknutím. předem díky
2x
Znáte vzorečky pro sinus dvojnásobného úhlu? Ty vám zde pomohou.
V prvním příkladě bych nejprve cotg 2x zapsal jako cos 2x / sin 2x, odstranil bych zlomky (vynásobil rovnici jmenovatelem) a pak už mi z toho snadno vylezevztah pro sin 4x
V tom druhém případě bych rozepsal levou stranu s použitím vzorce pro sin 2x a pro cos 2x a použil bych ještě goniometrickou jedničku. Celkově to ovšem vypadý složitěji než ten první, zkuse to a já se na to ještě mrknu.
doplněno 15.05.13 08:43:Koukám, že mezitím asa ten postup na první příklad rozepsal, takže to je hotovo Ten druhý je přeci jen složitější.
doplněno 15.05.13 09:36:Ono to zas tak složité není, jen se mi postup, ktewrý vidím, zdá trochu zkomplikovaný a hledám přímočařejši postup.
A jen poznamenám: to, co napsal asa, jakoby nevyužívá substituci, ale vlastně počítá sin 2x, takže substotuce (skrytá) by mohla být 2x = y
2x
Ta druhá rovnice taky není tak složitá, viz obrázek. Jen mě pořád zlobí, že můj postup nejprve vyjádří sin 2x, cos 2x pomocí sinu x a cosinu x a pak zase zpět. Ale přímočařejší cestu jsem prostě nenašel. (Vytčení se tam používá.)
Shrnutí použitých vzorců:
sin 2x = 2sin x cos x
cos 2x = cos² x - sin² x
cos² x + sin² x =1
a, pro úplnost. tg x = (sin x )/ (cos x)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.