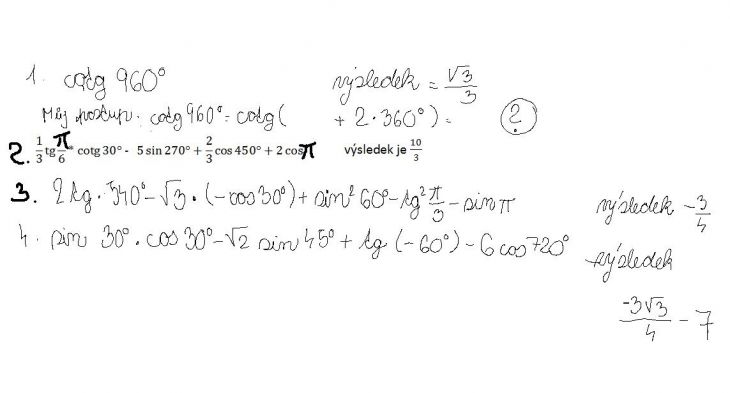Nejste přihlášen/a.
2x
Jen ještě doplním, že musíš psát buď radiány čili pouřívat obloukovou míru (psát tg ( π ), sin ( π/4 + 2π ) atd,) nepo se důsledně držet míry ve stupních: (cotg 960° = cotg ( 5*180° + 60° ) = cotg ( 60° ) atd.), nesmí se to míchat- /plně špatně by bylo třeba tg (45° + 3π ), ale dobře není ani třeba ... sin2 ( 60° ) – tg2 ( π/3 )...
A jinak samozřejmě je obecně tg ( x + kπ ) = tg (x) pro k celé (a x vyjádřené v obloukové míře), podobně pro cotg, u sinu obecně vzato platí sin ( x + 2kπ ) = sin x , podobně u kosínu, ale jsou tam ještě další vztahu, s jejichž pomocí převádíme úhel do "základního" intervalu <0,π/2>, pro který jsou psány tabulky a uváděny ty základní vztahy jako že sin π/4 = (čemu že?). Ty si zopakuj, namátkou uvádím sin (-x) = –sin x, sin ( π –x ) = sin x. Adalší, to jste se museli ušit, tak si je zopakuj.
0x
No počítat ti to nebudu. Třeba se někdo najde. Jethro či jiný.
Ode mne jenom rada.
1/ Vezmi tabulky a počítej.Některé goniometrické funkce jsou obecně známy i bez tabulek. Např. sin (30°) = 1/2
2/ Pochopitelně nejdřív je třeba si hodnoty "uzpůsobit"
Co to má být že cotg (960°) = cotg 2*360°)
Obecně cotg ale i sin,cosin,tg se nechá napsat že cotg ( x + k*Pí) = cotg (x) kde "k" je libovolné celé kladné číslo a to "Pí" je ti snad jasné, nebo taky 180°
Takže cotg (960°) = cotg (5*180° + 60°)
doplněno 01.05.13 12:26:A ten smajlík je pravá závorka
doplněno 01.05.13 12:30:Takže cotg (960°) = cotg (5*180° + 60°) = cotg (60°)
Promiň vypadla mi dvojka. Ten koeficient je pochopitelně 2*k*Pí
Takže
Takže cotg (960° = cotg (4*180° + 240° = cotg (240°
doplněno 01.05.13 12:58:Ještě lépe
Takže cotg (960° = cotg (2*2*180° + 240° = cotg (240°
doplněno 01.05.13 12:59:Koeficient "k" k = 2 a ´Pí = 180°
doplněno 01.05.13 13:10:Vidíš teď Ti to dovysvětlil "kartaginec". No já sám ani moc nepřemýšlel, že u tg a cotg stačí k*Pí a u sin a cosin 2*k*Pí. (záporné hodnoty)Ovšem ani u tg a cotg nelze použitím 2*k*´Pí nic zkazit
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.