Nejste přihlášen/a.
Dobrý večer,
chtěla bych Vás poprosit, zda by byl někdo ochotný a pomohl mi s těmito pěti příklady, prosím i o postup, pokud se najde někdo ochotný ![]() .
.
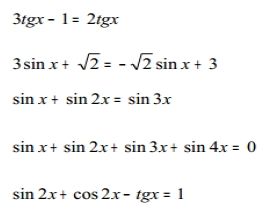
0x
Ono to není zase tak jednoduché. Jistě, první dva jsou vskutku elementární, ale ty další přeci jen vyžadují nějaké hlubši znalosti a triky. Hodí se snát součtové vzorce
sin (a±b) = sin a cos b ± sin b cos a
a vzorečky typu
sin a + sin b = 2[ sin (a+b)/2 ]*[cos (a-b)/2]
další viz pžiložený obrázek.

Také jsou užitečné vzorečky v jistém smyslu obrácené, viz další obrázek.
Zkus nad tím zauvažovat. Ono to půjde různě, zejména vzhledem k množství různých vztahů mezi goniometrickými funkcemi. Poradím, že u čtvrtého příkladu docela vtipný způsob začíná tím, že rovnici vynásobíme výrazem sin x/2.
Když nic, tak se k tomu ještě vrátím.

No většinou u těch školních příkladů při šikovné úpravě je výsledek jednoduchý. No přiznám se že u toho druhého příkladu kde dle mne je výsledek arcsin (0,36) se s těmi dvojčleny ve zlomku s plus i mínus se asi nic neudělá.
doplněno 26.04.13 21:49:A doplnil bych
sin 2x + cos2x = 1
sin 2x = 2sin x.cos x
Jak na to koukám s použitím vzorce by výslek 4. příkladu byl tg(x) = 0
Ten druhý vzorec je zvláštní případ vzorce pro sin(x+y), kde x=y.
ten první _ tam asi má být na druhou.
doplněno 26.04.13 23:16:K tomu výsledku příkladu 4: tg x = 0 by znamenalo x = kπ, což vyhovuje, ale docela by mne zajímalo, pomocí jakého vzorce. Mně vyšlo
(sin 2x)(sin 5/2 x) = 0, čemuž vyhovuje mimo jiné x = π/2, a to vyhovuje i původní rovnici.
Jinak opravdu bych čekal nějaký jednoduchý výsledek a to, na co jsem přišel, zas až tak jednoduché není, což mne mate.
doplněno 27.04.13 11:43:Jinak jsem stále připraven napsat víc, ale čekám na aspoň minimální reakci tazatele.
No ten první vzorec blbě opsáno. Jistě vždyť to je Pythagorova věta. No a tady má pá dalších vzorců s vícenásoným argumentem
doplněno 27.04.13 11:37: To tg(x)=0 je hloupost. To vyšlo s použitím sin 2x + cos2x = 1 když tento vzorec je sám o sobě hloupost.
No tazatelé si v poslední době zvykli nalajnovat příklady a pak čekat až jim to nějaký dobrák vyřeší
No pokud si neporadíš s druhým příkladem tak další jsou bez šance. Já to jen trochu to zkusil, nemám čas nad tím sedět, ale třetí a další příklad nevedou k jednoduchému řešení.
Snad u třetího příkladu je jeden kořen kdy sin (x) = 0 a pak dořešit cos (x) - 2 sin² (x) - 1 = 0
doplněno 29.04.13 23:24:Oprava
cos (x) + 2 sin² (x) - 1 = 0
doplněno 29.04.13 23:37:A co takhle úprava na
2cos² (x) - cos (x) - 1 = 0
a dořešit kvadratickou rovnici
doplněno 30.04.13 13:53:No ten tetí příklad není zas tak těžkej. Stačí použít 2 + 1 vzorečky s přiloženého odkazu a vyřešit kvadratickou rovnici. Vypadá to na trojnásobný kořen kdy sin (x) = 0 cos (x) = 1 cos (x) = -0,5
S tím mohu jen souhlasit, samozřejmě s tím, že u příkladu druhého je jednoduchá ta základní část, totiž vypočtení sinu, výpočet vlastního x už ne tolik. Nicméně aspoň ten začátek by tazatelka měla zvládnout a dál se pak uvidí,Ten třetí příklad by se asi řešil tak, jak uvádíš, s tím, žeodvození té kvadratické rovnice je možné různě, přitom krok 2., tedy výpočet x, když znám cosinus , je zase dost jednoduchý.
kE ČTVRTÉMU PŘÍKLADU JSEM JAKÝSI TYP DÁVAL, ALE TEN JE SICE VTIPNÝ A MNĚ SE LÍBÍ, ALE NEJSEM SI JIST, ZDA JE TI TA NEJJEDNODUŠŠÍ CESTA. mOŽNÁ BY BYLO LÉPE ZAČÍT TÍM, ŽE SEČTEME SIN X+SIN 3X A EXTRA SIN 2X + SIN 4X PODLE TĚCH VZOREČKŮ JIŽ UVEDENÝCH.
Omlouvám se za velká písmena, ale přepisovat to už nebudu.
Stále nic? Tak ještě nápověda s tím druhým. První krok bude výpočet sinu x. Možná vám pomůže, když si zavedete substituci sin x = w, Dostanete tak rovnici pro w, která bude možná pro vás trochu přehlednější:
3w + V2 = _V2 *w + 3
(V zde píši místo odmocniny)
odkud vypočtu w. To byste měla umět, to je lineární rovnice, tak sem napište výsledek a zapřemýšlejte, co s ním dál. Napište, co si myslíte nebo proč nevíte dál a pbavíme se
doplněno 01.05.13 09:47:.
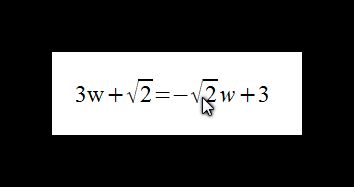
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.