Nejste přihlášen/a.
Dobrý den, prosila bych o vyřešení této rovnice.. mělo by to být přes logaritmování, nedaří se mi to vypočítat, prosím i s vysvětlením.. díky
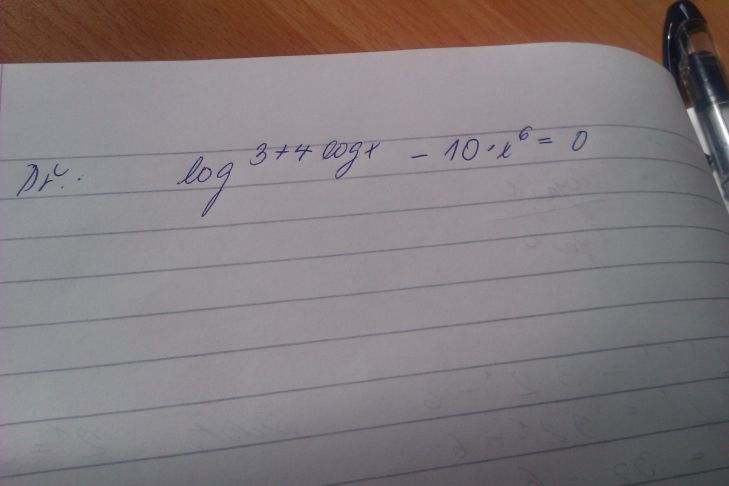
0x
Především je to nějaké divné zadání. Tak, jak je to zapsáno, to vypadá, jako by výraz 3 +4 log x byl v exponentu, ale v exponentu čeho? nebo jde o výraz
(log 3 ) + (4*log x)?
(Ty závorky jsem přidal, aby bylo jasno, co mám na mysli.) To by spíš mělo smysl, ale stejně; prosím upřesnit.
Takze v prepisu to ma vypadat takto:
log(-10x^6)^(3+4logx)=0
?
doplněno 25.03.13 17:49:Pardon. Vypadli zavorky.
Takto:
[log(-10x^6)]^(3+4logx)=0
?
0x
Kartaginec - prosím Vás, mohl/a byste mi pomoc s příklady podobného typu? Jedná se o pět příkladů. V té dvojce už to a) mám, ale zbytek už jsem ztracena. Děkuji mockrát za Vaši pomoc, moc si toho cením.

Jak se spocita ten priklad 2a)? ![]()
Dneska nejsem nejak ve sve kuzi. Ztratil jsem se i pri vypoctu toho prikladu 5a) ![]()
![]()
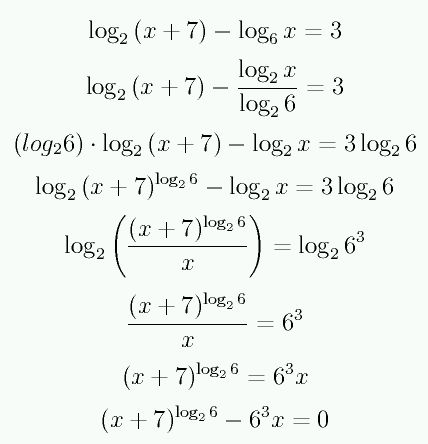
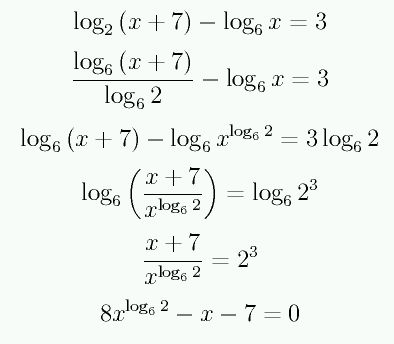
Jak říkám, přibližné řešení. Ale ten graf pěkně ukazuje, že můj kvalitativní rozbor byl správný. Díky.
Vypadá to hodně zamotaně, ale já se nedivím. Ono by to chtělo, počkat, až tazatel upřesní zadání. To, co napsal, rozumné upřesnění není.
Děkuji moc všem za snahu, to zadání je tak, jak je napsané, dostali jsme to ve škole vyřešit domů za jedničku, ještě jsme to nedělali a kdo na to jakože přijde, tak dostane jedničku..dnes jsme to kontrolovali a měla by z toho vyjít kvadratická rovnice a nějak substitucí výsledek to se pak dosadí a vyjde z toho konečný výsledek ve kterém je dokonce odmocnina, vůbec tomu nerozumím, naštěstí jdu po prázdninách na doučko..
Dobře, takže je tam logaritmus, ten logaritmus je umocněn na 3+4log x . A co je argumentem toho logaritmu? Co do něj dosadíme? Pokud jste to kontrolovali, tak na tuto otázku musíte umět odpovědět. Bez této odpověti se dál nepohneme.
0x
AD 1. k původnímu dotazu: stále čekám na upřesnění úlohy. Minimálně tam někde schází nějaká ta závorka. Upřesnění, že
"ano 3+4log x je v exponentu toho log" je nedostatečné, zbývá upřesnit co do toho logaritmu dosazujeme. Formálně nejpřirozenější by byla interpretace, kterou zvolil Axus, (čili doplnění závorky kolem "-10x^6"), bohužel výraz -10x^6 je stále záporný nebo nulový a tudíž ho nelze nikdy do logaritmu dosadit (alespoň v oboru reálných fonkcí) a vzniklá rovnice je k ničemu.v podstatěvychází z toho, že tazatyel nemáLuke zvolil jinou interpretaci, totiž, v podstatě, vychází z předpokladu, že tazatel si plete argument a exponent. I tak musel doplnit nějakou tu závorku, dostal se k rovnici, která má jakýsi smysl, ale řešit ji neuměl, což se vůbec nedivím. Na pohled, když si promyslím průběh těch funkcí, by řešení existovat mělo, dokonce jednoznačné asi, ale najít ho půjde nejspíš jen přibližnými metodamy; takže to asi nebude to, oč měl tazatel zájem.-K dotazu heyley dám další odpověď
doplněno 26.03.13 11:53:
opravuji překlepy:
K původnímu dotazu: stále čekám na upřesnění úlohy. Minimálně tam někde schází nějaká ta závorka. Upřesnění, že
"ano 3+4log x je v exponentu toho log" je nedostatečné, zbývá upřesnit, co do toho logaritmu dosazujeme. Formálně nejpřirozenější by byla interpretace, kterou zvolil Axus, (čili doplnění závorky kolem "-10x^6"), bohužel výraz _10x^6 je stále záporný nebo nulový a tudíž ho nelze nikdy do logaritmu dosadit (alespoň v oboru reálných fonkcí) a vzniklá rovnice je k ničemu. Luke zvolil jinou interpretaci, totiž, v podstatě, vychází z předpokladu, že tazatel si plete argument a exponent. I tak musel doplnit nějakou tu závorku, dostal se k rovnici, která má jakýsi smysl, ale řešit ji neuměl, což se vůbec nedivím. Na pohled, když si promyslím průběh těch funkcí, by řešení existovat mělo, dokonce jednoznačné asi, ale najít ho půjde nejspíš jen přibližnými metodami; takže to asi nebude to, oč měl tazatel zájem.
K dotazu heyley dám další odpověď
0x
Díky, tak to jo. Tohle je interpretace, které rozumím, ale to původní zadání je tak trochu nesmyslné.
Jinak skutečně nevím, proč se tento dotaz objevuje podruhé, nic lepšího se k tomu napsat nedá.
Psáno ln, bez indexu, je ovšem beze sporu přirozený logaritmus, zrovna tak jako log, psáno bez indexu, obvykle znamená Briggsův logaritmus. Je pravda, že ten indez č(míněno typograficky) se běžně připisuje k symbolu log, ale označení není zase tak úplne jednotné, občas se píše ln x pro dvojkový logaritmus, který se označuje někdy i lg x, a tak pokud dám k ln ten dolní index, mělo by to být srozumitelné. Nicméně je pravda, že log_k je nejběžnější a asi jsem to měl použít. Omliuvám se.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.