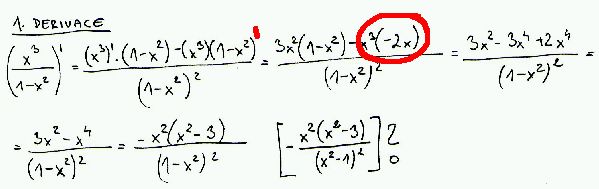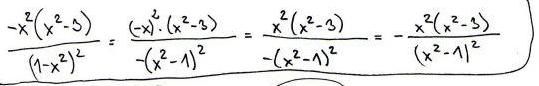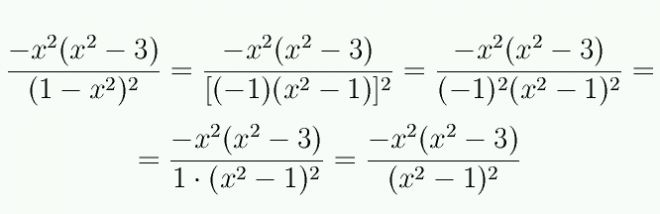Dobrý den, zkontrolovali a případně poradili byste mi někdo, prosím, s touto funkcí?
doplněno 29.01.13 23:48:Tady je můj postup řešení: imgupload.sk/...
doplněno 30.01.13 00:14: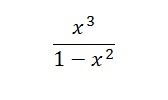
0x
Prvni derivaci mas spatne ( vzorec pro derivaci podilu).
Taky jsem nepochopil to cervene +/+. Protoze napriklad pro cisla (-1,0) to bude -/+ ![]()

Je to oskenované. A můžu se ještě zeptat, zda byste mi nezkontroloval tu druhou derivaci a asymptoty, prosím? U té druhé derivace nemůžu přijít k tomu konečnému výsledku, konečný výsledek je v hranaté závorce. Bude to nějaká úprava toho mého posledního výsledku zřejmě, ale nemůžu na to přijít, jak to upravit.
Ta hranata zavorka se dostane tak, ze nahore se vytkne -2x, v zavorce pak vyjde vyraz, kde se provede nahrada a=x^2 a vyresi se kvadraticka rovnice. Pak se ta zavorka prepise do tvaru (x^2-x1)*(x^2-x2), kde x1 a x2 jsou ty spocitane koreny a neco se tam pokrati se jmenovatelem.
Děkuju moc ![]() . Hned si tu úpravu zkusím.
. Hned si tu úpravu zkusím.
A můžu se ještě, prosím, zeptat? U té 1. derivace si nejsem jistá, proč je ve výsledku ve jmenovateli (x na druhou - 1)to celé na druhou. Mně to vycházelo (1 - x na druhou)to celé na druhou. Tam se dá to mínus z čitatele před celý zlomek a pak to mínus platí pro čitatele i jmenovatele?
A nějak si nevím rady, jak tu funkci zakreslit ve výsledku.
doplněno 30.01.13 07:23: Tak už jsem k tomu došla, k té hranaté závorce u 2. derivace. Děkuji za radu ![]() .
.
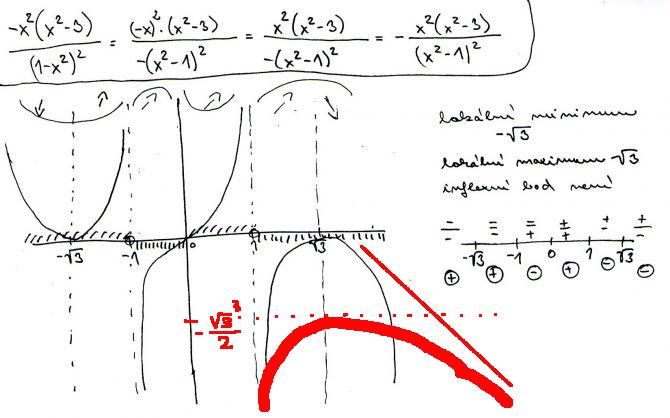
- prochazi bodem [0,0]
- je soumerna podle pocatku souradnic (tj. bodu [0,0]), protoze je licha
- v bode +1 je zleva +&inf; a zprava -&inf;
- v bode -1 jsi si ty asymptoty zapomnela spocitat, ale protoze vis, ze funkce je soumerna podle pocatku souradnic, tak muzes kreslit jen pravou pulku grafu ("od nuly doprava") a pak to jen stredove preklopit pro x<0
- znas intervaly, kde je funkce kladna ("nad osou x") a kde zaporna ("pod osou x")
- znas intervaly, kde funkce roste (prvni derivace je kladna) a kde funkce klesa (1.derivace zaporna)
- znas intervaly, kde se funkce "prohyba" smerem nahoru (konvexni) nebo dolu (konkavni)
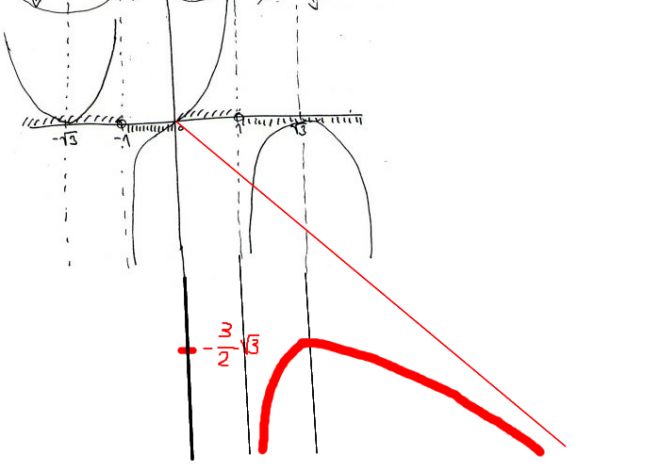
- jedine, co zbyva urcit, je, jak to bude vypadat kdyz se funkce vzdali od pocatku a tam se priblizuje primce se smernicii -1 (tedy pada pod uhlem 45° do nekonecna)
U té první derivace to bylo myšleno tak, jak to mám popsané na obrázku?
Zkoušela jsem tu funkci zakreslit a vyšla mi tak, jak je na obrázku a ještě jsem tam doplnila lokální min. atd.
doplněno 30.01.13 07:46:zapomněla jsem na obrázek
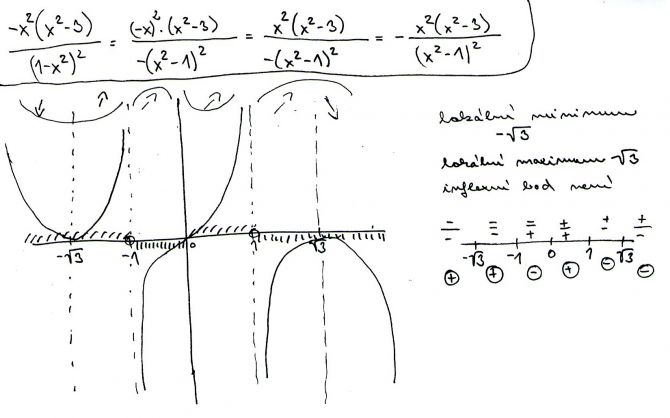
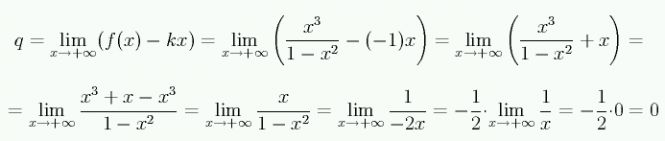
To jsem se snažila dojít k tomu výsledku u první derivace, jak jsem měla problém s tím jmenovatelem.
Je to oskenovanéKoukal jsem, ze je to v JPG. Nemas to jen tak pro zajimavost i v monochromatickem PNG? Zajimalo by me, jak velky by ten soubor byl. PNG by melo byt na podobny typ souboru (jednobarevne pismo na jednotnem pozadi) mnohem lepsi nez JPG.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.