Našla jsem příklad: Je pozemek kruhové plochy poloměru "R". Na obvod pozemku je zatlučený kolík a k němu uvázána koza
na provaze délky "r". Jakou plochu pozemku koza spase? (r < 2r).
doplněno 16.01.13 18:40:Obrázek:
2x
..."(r < 2r)"... - to už tak bývá... ![]()
Vzorec pro plochu kruhu znáš, ne?
Máš dva kruhy - o poloměrech R a r , potřebuješ plochu mezikruží - kde je problém?
doplněno 16.01.13 19:25:Ahaaa - sakrakruciš - to jsem se ´pěkně´ uťal - špatně jsem si otázku přečetl, omlouvám se...
![]()
´Šel´ bych cestou nalezení průsečíků kružnic a podle nich dopočíst plochy kruhových úsečí...
![]()
2x
Spočteme obsahy úsečí a jejich obsahy sečteme. Snad je postup zřejmý z obrázku.
doplněno 16.01.13 20:29:U výpočtu S2 má být správně úhel α2, jak plyne z obrázku _ modrá úseč.
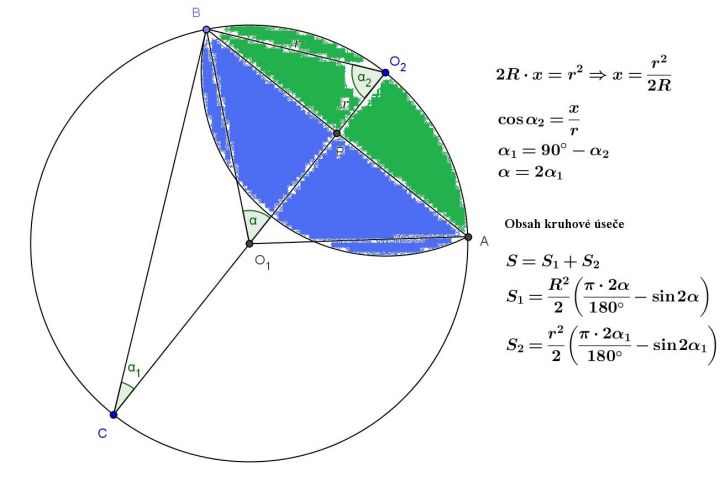
Úhel α2 se vypočte pomocí goniometrické funkce cos(α2) = x/r z pravoúhlého trojúhelníku O2BP, jak je zřejmé z obrázku. Úhel α1 je doplněk do 90° v pravoúhlém trojúhelníku CO2B.
Anebo lze oba úhly (respektive jejich goniometrické funkce) spočítat z pravoúhlého trojúhelníku O2BC. Možností je nepřeberně, každá má své výhody. Petapeta potřebuje spočítat x = |O2P|, zde uvedený postup potřebuje znát |BC|, případně oni to ne. A jde to ijinak, další postupy už ale asi budou složitější.
To vědět netřeba, stačí anát jejich siny a kosiny, které vypočteme z délek zobrazených stran pravoůhlých trojúhelníků. Vlastně potřebujeme počítat jen |AB|, ostatní potřebné je zadáno.
Vážení rádci, vaše rady jsou sice hezké, ale konkrétně nic neřeší. V naznačeném obrázku totiž kromě R a r nic jiného neznáme, tedy nevíme délky O2B, O2O, AB ani BC, aby bylo možno vypočítat příslušné úhly. Toje vlastně podstata úlphy - určit délky.
Ve skutečnosti tyto rady řeší vše, jen je třeba znát alespoň Pythagorovu větu. | O2B| = r, dále potřebujete buď |O2C| = R a |BC|, což je Pythagorova věta, nebo x = |O2P', což je Euklidova věta o odvěsně. Asi jsme se oba s petapetou domnívali, že tohle je trivialita, ale zřejmě tedy není.
Stačí tak, nebo potřebujete konkrétní výpočet?
doplněno 20.01.13 11:31:Navíc, když si uvědomíme, že sin α1 = cos α1 = r/2R, známe vlastně vše.
doplněno 20.01.13 11:32:Oprava: sin α1 = cos α2 = r/2R
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.