Moc prosím o pomoc. Už měsíc sedím nad tímto příkladem a absolutně si s nevím rady. Potřebuju ho k zápočtu 
. Je tady někdo,kdo tomu rozumí a byl by schopen to vypočíst? Nejde mi moc určit tak konstanta, vycházejí mi samé divná čísla a Fx 2 místo 1 ://. Potřebovala bych to do 5.1. Předem moc děkuji za jakoukoli snahu!
Náhodná veličina X je charakterizována hustotou
f(x)= 10*c*x^2 pro (0, 0.6)
9*c*(1-x) pro (0.6 , 1)
0 jinde
1/ Určete koeficient c
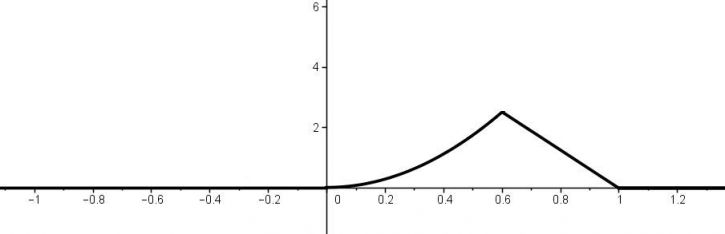
2/ Graf f(x) načrtněte
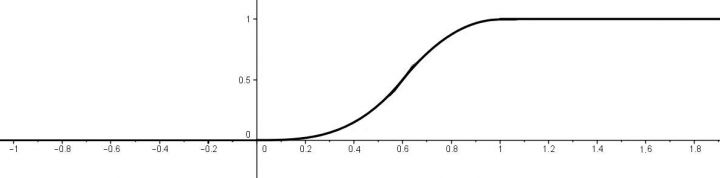
3/ určete F(x) a načrtněte její graf
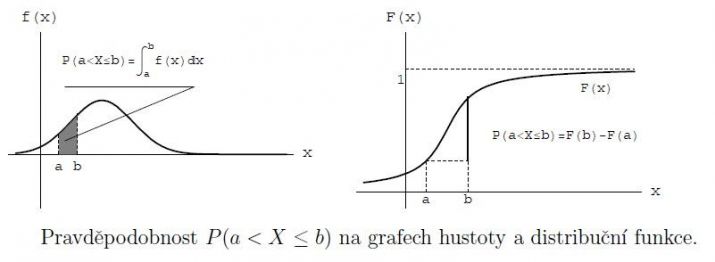
4/ pravděpodobnost, že NP nabývá hodnoty větší než 1,2; vyznačte na obou grafech
5/ pravděpodobnost, že NP nabývá hodnoty mezi 1,7 a 2,5; vyznačte na obou grafech
6/ distribuční funkci v bodě 1,1
7/ distribuční funkci v bodě 3,59
0x
Vašemu zadání tak úplně nerozumím. Co má být zkratka NP u 4/ a 5/? A co má znamenat "mám limit jen do 0 do 1?
Hustotu pravděpodobnosti máte zadanou a je zapotřebí určit distribuční funkci F(x).
Zdali jsem se nespletl, tak by to mělo být nějak takto:
Pro x ∈ (−∞, 0) je f(x) = 0 ⇒ F(x) = 0
Pro x ∈ <0, 0.6) je f(x) = 125/18 x2 ⇒ F(x) = 125/54 x3
Pro x ∈ <0.6, 1) je f(x) = 25/4 (1_ x) ⇒ F(x) = _25/8 x2 + 25/4 x _ 17/8
Pro x ∈ <1, &infin
je f(x) = 0 ⇒ F(x) = 1
Takhle mi vychází graf f(x):
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.