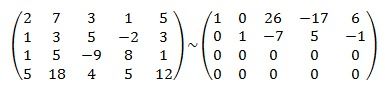Dobrý den, mohli byste mi, prosím, někdo poradit s těmito příklady? Přikládám zadání a můj postup řešení. Předem děkuji za případnou ochotu.
doplněno 02.01.13 14:45:zadání
doplněno 02.01.13 14:53:zadání 2
doplněno 02.01.13 14:53:zadání 3
doplněno 02.01.13 15:02:zadání 4
3x
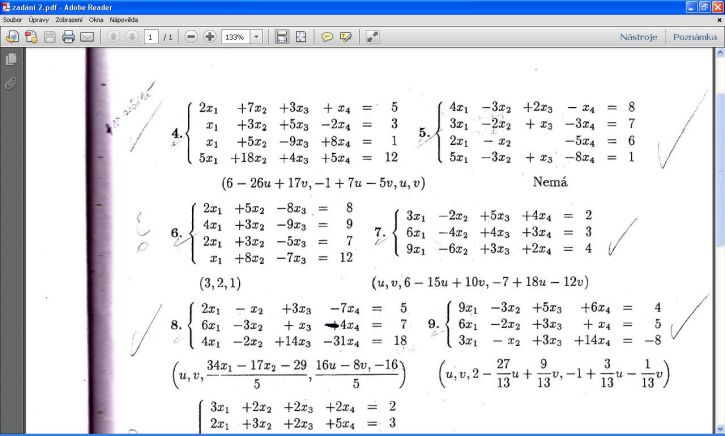
V př. 6 jsou zadány 4 rovnice pro 3 neznámé. Hodnost matice soustavy i hodnost rozšířené matice soustavy je rovna počtu neznámých, tj. n = h = hr = 3, proto má soustava jediné řešení. Z upravené matice je zřejmé, že x1 = 3, x2 = 2, x3 = 1. Jedna rovnice je zbytečná, je lineární kombinací zbývajících.
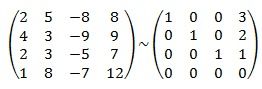
Děkuji moc za radu, tento příklad mi zrovna vyšel. Měla jsem problém s příkladem číslo 6. Chtěla jsem zde vložit obrázky zadání více příkladů a napsat, s kterými jsem měla problém, a pak i obrázky mých postupů, ale nějak jsem měla problém s vkládáním více obrázků. Mohla byste mi případně, prosím, poradit s tím příkladem 6? Já ho upravovala na trojúhelníkový tvar, ale nakonec mi tam vyšly samé nuly a k tomu jeden zlomek, kterého se mi nedařilo zbavit.
A ještě bych se zrovna chtěla zeptat, zda matice a determinanty jdou vždy vypočítat přes trojúhelníkový tvar anebo musím u některých příkladů použít i jiný postup než trojúhelníkový tvar?
Té poslední otázce moc nerozumím. Matice je něco jiného než determinant. Matice je obdélníkové schéma, které je vytvořeno z čísel, kdežto determinant je číslo. Pro počítání s determinanty nemůžeme používat stejné úpravy jako pro matice. Lineární rovnice můžeme řešit pomocí matic nebo pomocí determinantů, ale oba způsoby se od sebe značně liší.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.