Nejste přihlášen/a.
Mám dva obdelníky o různém obsahu a mám narýsovat čtverec o stejném obsahu (OBECNĚ, BEZ ZADANÝCH ROZMĚRŮ)
0x
Tak mne napadá:
1) Použitím Euklidovy věty o výšce (Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníku je roven obsahu obdélníka sestrojeného z obou úseků přepony.) nejprve převedu obdélníky na rovnoploché čtverce. (Šla by použít i Euklidova věta o odvěsně _ Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníka je roven obsahu obdélníka sestrojeného z přepony a úseku přepony k této odvěsně přilehlé _ ale to by bylo trochu složitější. V obou případech budu potřebovat ještě Thaletovu větu.)
2) Následně tyto čtverce sečtu pomocí Pythagorovy věty.
Jo,jo něco takového to bude. Ale musím to narýsovat, takže mám ty dva obdelníky dát vedle sebe? Aby se dotýkaly jsou stranou?
Těžko říci. Ty rovnoploché čtverce, to jsou vlastně dvě nezávislé úlohy a mohl bych je tedy nezávisle narýsovat a výsledné čtverce následně "sečíst" někde vedle. Nebo bychom mohli tu Euklidovu větu použít na "odvěsnách: k sobě kolmých, které by se protínaly v patách příslušných výšek. Tím by příslušné ýšky tvořily rovnou odvěsny hledaného pythagorejského trojúhelníka. Tím bycho to dostali do jednoho obrázku, ovšem za tu cenu, že by mohl být trochu nepřehledný.
0x
Tak jsem to zkusil načrtnout, ale je to nepřehledné. Připojují obrázek s obdélníky, se kterými budu v další odpovědi pracovat.
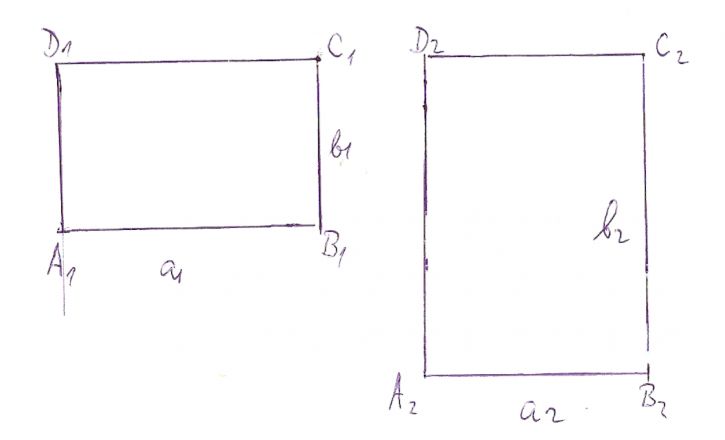
Tak teď jsem napsal podrobný popis a jedním chybným klepnutím ho smazal. Znovu ho psát nebudu, jen přidám obrázek a budu doufat, že ho pochopíte. Konec konců tohle má být návod, ne řešení.
doplněno 30.12.12 16:56:Jen oprava, místo D2' má být C2'
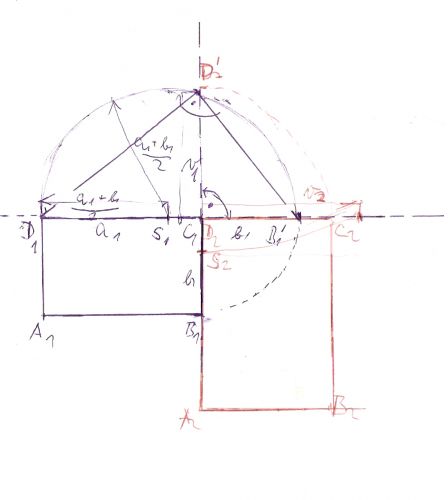
Ve středu úsečky D1B1' (pro první obdélník), tedy ne středu té přepony, kterou nbudete využívat v Euklidově větě o výšce.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.