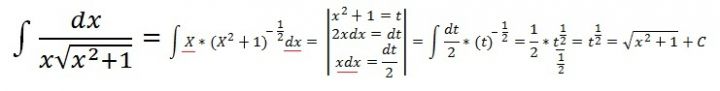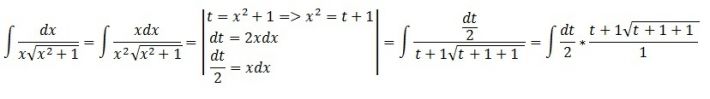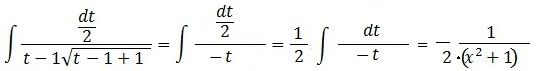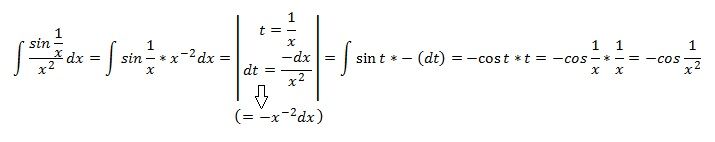pls. help, kdo by mi poradil jak je vypočíst?, pravděpodobně substitucí, ale nejsem si jistý jak na ně.
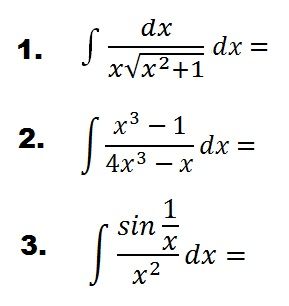
0x
Podle me to vypada na ukazkove priklady na metodu "per partes" 
V tom prvnim prikladu asi nema byt dvakrat dx. 
Jinak by jsi musel mit snad dvojity integral, i kdyz s takhle psanou dvojitou integraci jsem se nesetkal. Na druhou stranu nejsem matematik
Napr. 2. priklad: int (u.v) dx, kde u = (x^3 - 1) a v = (4x^3 - x)^(-1) (na minus prvni).
0x
To jde různě.
V tom prvním příkladu je skutečně jedno dx navíc a je ho třeba škrtnout.
U prvního intedrálu funguje substituce sqrt(x² + 1) = x + t, (sqrt... druhá odmocnina), případně substituce x = tg t. A tady konkrétně by možná pomohla i substituce x²+1 = y. Ake vyžadovala by ještě následné úpravy.
Druhý příklad je racionální funkce. Standardní postup sočívá v částečném vydělění tak, aby stupeň čitatele byl nižší než stupeň jmenovatele, a v následném rozkladu na parciální zlomky.
Třetí příklad vyjde velice jednoduše po substituci y = 1/x, dy = -dx/x².
U 2.př. právě nevím jak to lze vidělit když jsou stejné exponenty x˄3. Aby to šlo vydělit na parc.zlomky musí být přece v čitateli větší mocnina. Nebo to lze? (x˄3)
x˄3)=1?
Od toho je právě to částečné dělení. Vašemu zápisu moc nerozumím, místo smajlíku asi má být : ( (to editor občas dělá( a asi tím chcete to částečné dělění naznačit. Jste zřejmě na dobré stopě, jen při tom částečném dělění vám vyjde 1/4 + zbytek, a ten zbytek už má stupeň nižší než 3
Není. x máte ve jmenovateli, abyste do čitatele dostal x dx (což pak víceméně nahradíte tím dt) musíte zlomek proměnnou x rozšířit. Budete pak mít ve jmenovateli, krom té odmocniny, ještě x2, což vypočtete z té substituce jako t + 1. Nakonec bude vhodné zavést ještě další substituci t = y2 (y> 0) a převést to nea racionální funkci.
omlouvám se za přepis, samozřejmě je x² = t _ 1. Pak už ta substituce t = y² dává smysl a odstrní odmocninu. Jen nechápu, z jakého důvodu jste přehodil jmenovatel do čitstele? Nemáte tam přece dělení zlomků; když, tak násovení.
No comment. Tohle nemůžete myslet vážně.
doplněno 13.12.12 09:51:Omlouvám se, ale ono tohle opravdu je téměř neuvěřitelná sbírka chyb.
Za prvé, x² = (t_1), a jelikož tím x² násobíte tu následující odmocninu, musíte to tam opsat i s tou závorkou.
2. Tuhle úpravu vúbec nechápu, v každém případě zmizení odmocniny v tomto okamžiku nelze nijak odůvodnit.
3. přechod od předposledního výrazu k poslednímu také nedává smysl. Nejde o to, že jste přešel od t k x, to by mělo být prostě zkrácení zápisu, ale takhle přeci nevypadá integrál z 1/t.
4. Neurčité integrály lze obecně kontrolovat zkouškou, když výsledek zderivujete. Takovou zkoušku vám obecně doporučuji. A když se vám zdá tato zkouška příliš složitá, aspoň zauvažujte: dovedete si ppředstavit, jak derivováním racionální funkce vznikne výraz, ve kterém je proměnná v odmocnině?
Naskenoval jsem vám postup, vlastně celý vápočet. viz obrázek.
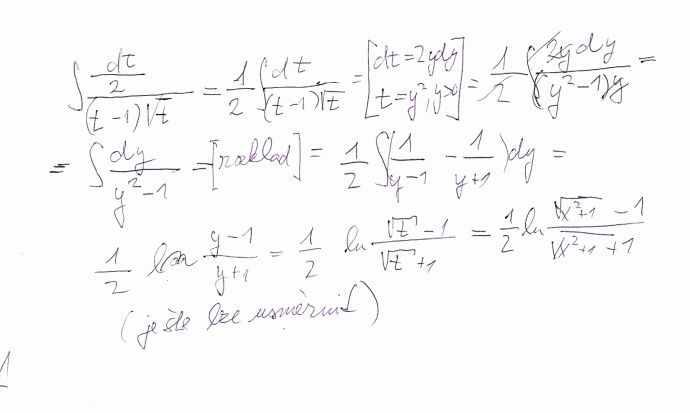
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.