dobrý den, prosím o pomoc u příkladu:
sestroj sdružené průměty rotačního kužele v rovině x(-7;5;6), vrchol V(-1;9;8) a podstavná kružnice prochází bodem M(1;?;1)
neumím vyřešit sestrojení středu elipsy, děkuji za pomoc
doplněno 17.12.12 14:48:můžu ještě poprosit o pomoc?
zadání mám sestroj sdružené průměty jehlanu s pravidelnou šestibokou postvavou v rovině r(-2;-6;2) vrchol na podstavě A(2;3;?), vrchol tělesa V(-5;4;9)
zase nevím, jak sestrojit alespoň druhý bod na podstavě (chápu, že jsou to asi triviální dotazy pro toho, kdo tomu rozumí, ale na přednáškách jsem měl podstatně lehčí zadání a ani na internetu jsem postup nenašel... díky
doplněno 28.12.12 07:35:a poslední prosba
zadání: bod C(-1;0;1) B(-1;6;1) A(4;5;4) přímka a= AB, přímka b= BC
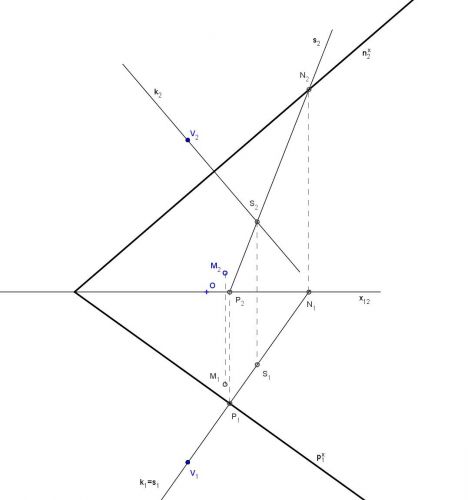
neumím sestrojit stopy roviny... ![]()
2x
Osa rotačního kužele je kolmá na rovinu podstavy, ne? Sestrojte průsečík přímky s rovinou a půl díla je hotovo. ![]()
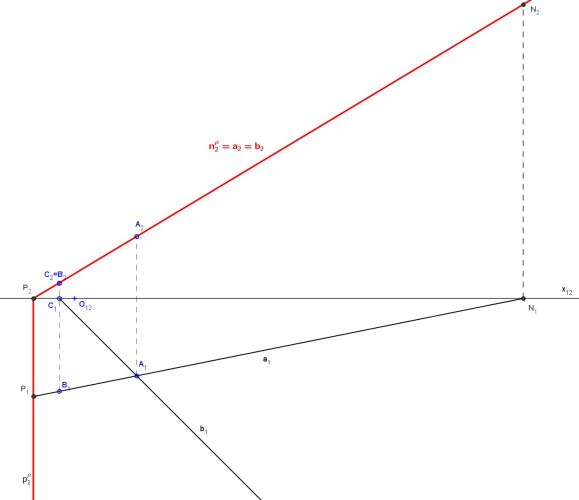
no tak půl díla máme hotovo, teď zjistěte skutečnou vzdálenost průsečíku osy s rovinou a bodu na elipse. To je poloměr podstavy kužele. V průsečíku osy a roviny nakreslete kružnici o poloměru podstavy, tím dostanete delší osu elipsy.
Máte střed elipsy, delší osu elipsy a bod na elipse. Z takového zadání snad elipsu uděláte i bez poradny.
0x
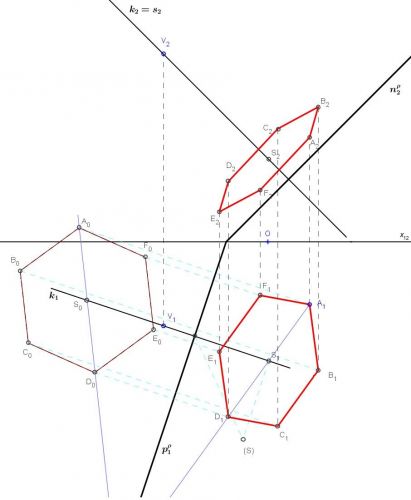
Střed podstavy nalezneme stejným způsobem jako u předchozího příkladu. Rovinu podstavy otočíme do průmětny. Stačí otočit střed podstavy kolem stopy roviny. Abych dostal poloměr otáčení, tak jsem si sklopil střed S do průmětny. Vrchol A0 šestiúhelníka jsem získal pomocí afinity. Nyní můžeme sestrojit skutečný šestiúhelník. Mezi otočeným šestiúhelníkem a jeho průmětem je vztah osové afinity, takže pomocí afinity sestrojíme body A1, B1, C1, D1, E1, F1 a z nich můžeme odvodit druhé obrazy A2, B2, C2, D2, E2, F2
doplněno 17.12.12 21:00:.
Bod A1 je již dán, takže jej již znovu sestrojovat nemusíme.
doplněno 17.12.12 21:11:Jinak na internetu je toho o Mongeově promítání dost. Například konstrukce šestiúhelníku jsem nalezl hned zde: http://1url.cz/JePP
doplněno 17.12.12 21:20:Nebo zde je pěkná učebnice: mdg.vsb.cz/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.