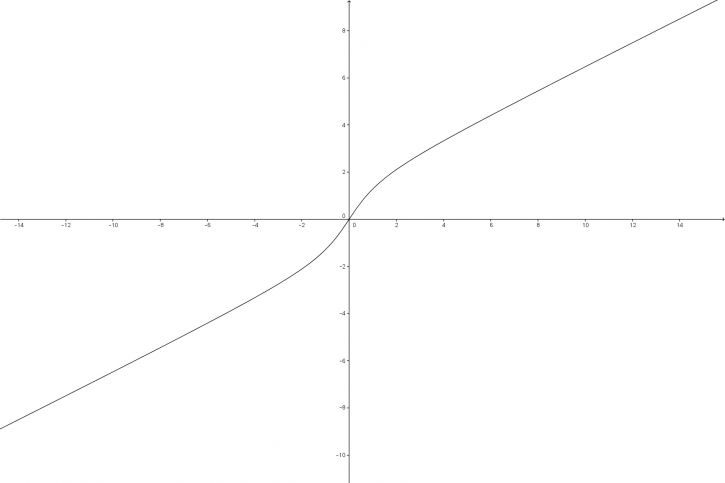
Zdravím, můžete mi prosím říct, jestli mám dobře průběh funkce u f-ce: (x/2)+arctanx?
D(f)=R
lichá f-ce
průsečíky s osami: Px=[0,0], Py=[0,0]
periodická s periodou kπ
body nespojitosti nejsou
f-ce je rostoucí od -∞ do +∞
nemá extrémy (lokální max. a min)
asymptoty: existuje vodorovná asymptota, neexistuje asymptota rovnoběžná s osami a neexistuje ani šikná asymptota
1x
Vodorovná asymptota, jak píše b, neexistuje, tu by měla ta arctangenta. Díky přičtené lineární funkci existuje šikmá asymptota (tak šíkmá, jak šikmá je přímka (x/2) ) .
Jinak bývá ještě zvykem vyšetřovat konvexnost, konkávnost, inflexní body.
díky 
, jo to jsem zapomněla připsat, vyšlo mi že je konkávní, protože po třetí derivaci je výsledek 1/2. U té šikmé asymptoty je výsledek 1/2? Ty inflexní body čitatel nemá a u jemnovatele mi vyšlo tohle: x1=-1 x2=1 aspoň myslím, protože tohle počítám poprvé
Tak to vyšlo špatně. Funkce je konkávná pro nezáporné x, konvexní pro záporné x, v nule má inflexní bod. Třetí derivací jste nějak špatně spočetla, nemůže být konstanta, to by funkce sama byla polynom. Když tak sem dejte svůj výpočet a opravíme ho. (Navíc konvexnost a konkávnost se určuje podle druhé derivace.). Tvrzení, že čitatel nemá. nflexní bod a u jmenovatele vám něco vyšlo, nějak nerozumím, Především nevím, co je čitatel a jmenovatel zkoumané funkce, a inflexní bod hledáme pro celou funkci. Tomu dotazu na šikmou asymptotu taky tak úplně nerozumím, je to tak, že v plus nekonečnu má funce asymptotu y = x/2 + π/2, v mínus nekonečnu pak y = x/2 - π/2
no druhá derivace je toto: -(2x/(x^2+1)x^2) takže sem dala proto že čitatel 2x=0 a tudíž x=0 a u jmenovatele jsem to myslím tak spíš tipla, protože jsem podobný příklad viděla někde jinde, kde měli uplně ten samý jmenovatel, akorát místo + bylo - a vyšel jim iflexní bod x1=1 a x2=-1 Proto jsem to jenom převrítila ty znaménka u inflexních bodů.
A s tou asymptotou si už vůbec nevím rady, ale děkuju, že mi pomáháte
Tak si to rozeberme. Jednak se trochu nepřesně vyjadřujete, takže mluvíte o čitateli a jmenovateli, máte na myslo derivaci, ale to jste neřekla a funkce původní není zlomek, proto jsem nechápal, o jaký čitatel a jmenovatel vám je.
Když jsme si toto vyjasnili, přejděmež k těm derivacím. Druhou derivaci máte dobře, první asi taky, jinak by vám ta druhá nevyšla (jen pro úplnost, první derivace je rovna f`(x) = (1/2) + 1/(x^2+1) pro všechna reálná x.) Třetí derivace - tam jde zřejmě zase o nepřesné vyjadřování, chtěla jste asi říci, že hodnota třetí derivace v bodě nula je 1/2, což mimochodem není tak docela pravda, ona je to -(1/2), ale aspoň víme, o čem mluvíme.
Tím jsme si vyjasnili pojmy, a teď co tyto pojmy znamenají. Je-li první derivace kladná. respektive záporná na nějakém intervalu, je funkce na tomto intervalu rostoucí, respektive klesající. Je-li derivace v nějakém bodě rovna nule, funkce sama může (ale nemusí) mít lokální extrém; zda ho má a jaký, určujeme obvykle podle znaménka druhé derivace. Ve vašem případě je první derivace všude kladná a správně jste tedy uzavřela, že
f-ce je rostoucí od -∞ do +∞nemá extrémy (lokální max. a min)
Konvexnost, konkávnost, inflexní body studujeme podle druhé derivace. Konkrétně: Je-li druhá derivace na nějakém intervalu kladná, je funkce na něm konvexní,je-li na intervalu záporná, je na něm konkávní. Je.li v nějakém bodě nulová a třetí derivace je tam nenulová, je tento bod inflexním bodem (což graficky znamebá, že v tomto bodě se funkce mění z konkávní na konvexní nebo naopak, nebo též že graf v tomto bodě přecházi z jedné strany tečny na druhou. (Ono to může být i trochu složitější, nemluvil jsem například o tom, kdy je v daném bodě třetí derivace nulová, ale pro naše účely to stačí.Tím bych pro začátek skončil, zkuste se na příklad podívad z hlediska těchto znalostí. Snad jen připomenu, že ten podobný příklad musíte brát s rezervou, ten rozdíl mezi plus a mínus je velmi podstatný, a krom toho z toho lehkého náčrtku se mi zdá, že v tom máte ještě najaký zmatek, ale to bych musel znát podrobnosti. A co se týče asymptoty, tomu věnuji někdy později samostatnou odpověď, zde snad jen tolik, že asymptota je přímka (taková, která se ke grafu funkce "přimyká v nekonečnu".
Takže když druhou derivaci dám =0, tak to číslo, které mi z rovnice výjde je inflexní bod? Chápu to dobře, že když první derivace je kladná a ta druhá je záporná, tak to znamená že existují inflexní body?
Takhle bych to netvrdil. Dá se říci, že čísla., které vyjdou z 1. derivace=0, nezridka byvaji extremy funkce. Někdy to mohou být i inflexní body, v tom případě to ovšem nejsou extrémy funkce.
To první je taková skoro pravda; je to jako s lokálním extrémem: lokální extrém počítáme typicky tak, že položíme první derivaci rovnu nule a to číslo, které mi vyjde, je bod, ve kterém může (ale nemusí! ) být extrém. Nnásledne spočteme druhou derivaci v tomto bodě a pokud je kladná, je v něm minimum ("jdeme do kopce"); pokud je záporná, je tam maximum ("jdeme z kopce").. Když je v tom bodě druhá derovace nula,pak jen na základě této informace nevíme nic a nastupují jemnější metody, se kterými to tu nebudu zatěžovat.
Podobně bod, ve kterém je druhá derivace nula, může, ale nemusí být inflexní bod. Jestliže je třetí derivace v tom bodě nenulová, (jedno, zda kladná či záporná). tak to je inflexní bod, je-li nulová, nevíme nic.
A ta poslední věta není dobře. Když už, tak je to tak, že je-li druhá derivace někde kladná a někde záporná (a první derivace si dělá co chce), tak někde mezi tím bude inflexníbod; ale to ber s rezervou, aby to bylo opravdu dobře, musel bych to vysvětlit podrobněji.
No a v našem případě, když vyšetřujeme druhou derivaci, neptáme se zda čitatel či jmenovatel má či nemá inflexní bod, to na funkci jako takovou nemá vliv a je to informace na nic. Ptáme se na znaménko druhé derivace, a to poznáme podle znaménka čitatele a jmenovatele. Nějdřív ze všeho se musíme zeptat, kde druhá derivace existuje, zde zjišťujeme, zda jmenovatel není nula. V našem případě není nula nikdy, dokonce je jmenovatel vždu kladný, takže derivace (druhá) exituje vždy a její znaménko je stejné jako znaménko jmenovatele, což je -2x. Takže v bodě x = 0 vznikne podezření na inflexní bod, třetí derivace je tam nenulová, podezření se potvrdilo. Pro x > 0 je čitatel záporný a funkce je konkávní, pro x < 0 je čitatel a (tedy celá druhá derivace) kladný a funkce je konkávní.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.