Nejste přihlášen/a.
Dobrý den, prosím vás o radu:
log _(1/2) (6+x) - log_(1/2) (2+3x) + 1 + log_(1/2)(x) = 0
log_(1/2)(6+x ) * (1/2) *(x) /( 2+3x) = 0
Takhle to asi nebude, děkuji za pomoc.
Když pokračuji dál:
[(6+x) *(x/2)] / (2+3x) = 0
upravím a odstraním zlomek
6x + x^(2) = 0
x(6+x) = 0
x=0
x=-6
Ale měl by vyjít jeden kořen 2.
Děkuji moc.
Tvoje chyba je pri odstranovani toho logaritmu. Obe strany rovnice jakoby prevedes do exponentu zakladu (1/2) ("umocnis" tou 1/2). Tim ti na leve strane vypadne ten log a na prave strane budes mit co?
Stále mně to nevychází:
log_(1/2)[(6+x) *(x)] / (2+3x) = 1
zase tam mám chybu, ale nevím kde. Díky.
Predtim jsi to mel skoro dobre, akorat jsi si neuvedomil, ze neco umocnene nulou je jedna, a ne nula, jak jsi mel ty na te prave strane.
Vychazejme z druheho radku v tvem puvodnim dotazu:
- obe strany povysime na mocninu jedne poloviny (tedy zakladu toho logaritmu)
- na leve strane rovnice budes mit vyraz typu a^log_a(b) a vpravo budes mit (1/2)^0
- upravou leve strany podle "meho" vzorce z 15:25 ti vyjde "b" (neboli stejna leva strana, co jsi psal uz v 09:08) a na prave strane ti vyjde 1 (to je ten jediny rozdil, na ktery jsem te upozornoval: neco na nultou je jedna a ne nula, ja jsi mel ty)
- dopocitas tuto jednoduchou rovnici
- vyjde ti spravny vysledek
![*uspech*]( "*uspech*")
Za ukol si tu puvodni rovnici ze zadani spocitej tak, ze na leve strane si nechas jen logaritmy a na pravou si prevedes normalni cisla. Tak je to v praxi jednodussi, protoze nemusis ta normalni cisla prevadet na logaritmy. Rozepis si to a uvidis.
Zkusím znovu od začátku:
log _(1/2) (6+x) - log_(1/2) (2+3x) + 1 + log_(1/2)(x) = 0
log_(1/2)[ (6+x) * (x) / (2+3x)] = 1 /v 09.08 jsem měl špatně napsáno * x^2, teď jsem dal jen (x) - týká se log_(1/2(x).
odstraním zlomek
6x+x^2 = 2+3x
x^2+3x-2=0
je to špatně, asi to vzdám, děkuji za Vaši ochotu a trpělivost.
log_(1/2)(6+x ) * (1/2) *(x) /( 2+3x) = 0 ... to máte dobře
log_(1/2)(6+x ) * (1/2) *(x) /( 2+3x) = log_(1/2)(1) ... místo 0 píšeme log 1, což je nula
(6+x ) * (1/2) *(x) /( 2+3x) = 1... místo 0 bude 1 a zapomněl jste na 1/2
doplněno 17.11.12 18:50:Takže zde vám chybí jen ta 1/2.
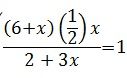
Děkuji Vám, na tu 1/2 jsem nezapomněl, já to totiž nevím, že se to tak musí psát, myslel jsem si, že když se s tím nepočítá u těch předchozích (6 + x) a (2+3x), tak že se s tím neuvažuje ani tady, tak díky moc. A ještě prosím, jak se převáděla ta jednička na pravou stranu, tam se nedává mínus?
Jedničku jste upravil správně, log½ (½) = 1. Kdyby na pravé straně by tedy byla _1, pak bychom mohli psát log½(2) = _1, neboť (½)-1 = 2.
doplněno 17.11.12 20:51:Pravá závorka se změnila v smajlíky.
Moc se Vám omlouvám, že jsem to stále nechápal; začátek jsem měl dobře, ale nevědomky. Půlku jsem tam dal proto, že jsem převáděl tu jedničku, takže to se týkalo jedničky, která měla být na pravé straně, ale to já jsem nevěděl, všechno jsem chtěl mít na jedné straně. Takže ještě jednou děkuji mockrát.
doplněno 17.11.12 21:04:Omluva patří i Luke 237.
Hlavne ze to ted chapes. Me jen zmatlo to, ze hned ve tvem druhem prispevku jsi to mel skoro naprosto spravne, jen s jednou malou chybickou a pritom v nasledujicich prispevcich jsi se ztracel cim dal tim vice. Ted uz vime, ze ta tvoje puvodni skoro-spravna rovnice byla nahoda Asi sem take zacnu vkladat takove hezke obrazky jako Petapeta
luke237, petapeta
Ráno moudřejší večera. Až teď mně všechno došlo jak to bylo. Poprvé po uvedení příkladu, jsem to měl správně, jak mě upozorňoval luke,jen na pravé straně místo nuly měla být "1". A to je ta příčina. Myslel jsem si, že mně nabádáte, abych místo "log_1/2(x)" dal do výpočtu na levou stranu "1/2(x)" a "1" z levé strany dal na pravou stranu a tohle jsem nechápal a nedovedl jsem z toho vycouvat. Proto mně bylo divné, že jednička z levé strany se přesouvá na pravou bez změny znaménka. Teď už vím, že se to týkalo jen nuly na pravé straně, kterou jsem nepřeměnil na jedničku. Někdy se do toho zamotám a nevím jak z toho ven. Ještě jednou velký dík oběma za nezměrnou trpělivost.
To prevedeni jednicky na pravou stranu jsem take doporucoval (v 16:39). Ten vypocet je pak jednodussi (nemusis prevadet cisla na logaritmy a pak zase se toho logaritmu zbavovat).
V kazdem pripade jsi s timto prikladem stravil vice casu nez kdokoliv jiny ze tveho okoli a to ti jiste umoznilo ziskat detialni prehled o tom, jak rovnice s logaritmy resit Vsadil bych se, ze do konce zivota nezapomenes, jak pracovat s logaritmy. 
Mezi kamarady budes snam jako ten, co "rozumi logaritmum"
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.