Dobrý rád,
rád bych touto cestou požádal o pomoc s výpočtem matematického příkladu.
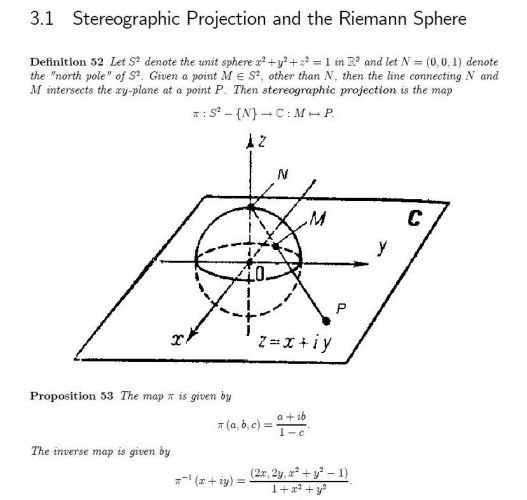
Syn dostal příklad: Nalezněte souřadnice x,y,z komplexního čísla 2+2i na sféře o poloměru 1 při stereografické projekci.
Děkuji předem za Váš čas
0x
: [x,y,z] = [cos45, sin45, 0] = [1/sqrt(2), 1/sqrt(2), 0]Predpokladam, ze ted asi budeme muset pockat na nekoho, kdo opravdu vi, jak se pocita ve stereoskopickem zobrazeni 
Ted jsem o tom jeste trosku premyslel a ten vysledek vyse je na 100% spatne! 
Nejak jsem si totiz neuvedomil, ze 2+2i nelezi na dvojkove kruznici 
Budu muset nad spravnym vysledkem jeste trosku zapremyslet. Prece jen by to chtelo nekoho, kdo umi se stereoskopickym zobrazovanim bezne pocitat, abych nemusel celou teorii kolem toho ted vymyslet
Uz jsem tu chybu nasel. Uhel θ merim od roviny (x,y) a ne od osy z, takze ty prevodni vztahy jsou trosku jine: [x, y, z] = [r * cosθ * cosφ , r * cosθ * sinφ , r * sin&theta]. Po dosazeni vyjde priblizne: [0,2418 ; 0,2418 ; 0,3420] 
Tento vysledek uz bych u zkousky predlozil jako spravny 
Moc si vážím Vaší pomoci. Jenom jsem chtěl poprosit, jestli mi pak ten kompletní výpočet (krok za krokem, jak jste počítal) napíšete do Wordu a pošlete na email, který jsem uvedl. Děkuji moc za Váš čas.
Ja ani nevim, jestli ten vysledek je spravne. Je to jen muj nejlepsi odhad. Berte to jako prvni vypocet od cloveka, ktery teprve pred dvema hodinama zjistil, co je to vlastne stereoskopicke zobrazeni
K vypoctu jsem pouzil jen zakladni znalosti komplexnich cisel ( vypocet magnitudy/velikosti a uhel komplexniho cisla) a trigonometrii (jeden cotangens a pak soucet uhlu v trojuhelniku). Tim my vysly sfericke souradnice bodu na plose koule a ty jsem pak prevedl na kartezke. Vsechny vztahy jsem si odvodil z obrazku, ktery jsem zminil jiz vyse.
Delal jsem to takhle primitivne z toho duvodu, ze me nic lepsiho nenapadlo. Jsem si jisty, ze urcite existuji prime vzorce pro prepocet hodnot.
0x
Je-li bod P obraz komplexního čísla 2 + 2i, pak na sféře bodu P odpovídá bod M o souřadnicích
M = [(2⋅2)/(1+22+22); (2⋅2)/(1+22+22); (22+22-1)/(1+22+22)] = [4/9; 4/9; 7/9].
Moc děkuju, ale chtěl jsem Vás poprosit, zda byste mi to nepřepsal do Wordu i s kroky, jak jste postupoval a následně poslal na email: IANKYS@centrum.cz
Vím, že už toho chci moc, ale moc by nám to pomohlo.
Děkuju
"Obdivuji"některé tazatele co by si snad od "rádců"nejraději nechali snad i utřít zadek.
Platí dvě pravidla
1/ Snažit se sám
2/ Hledat
a pak se teprve ptát. No a když Ti to strčil až pod nos tak zdroj musíš nají během půlminuty.
PetaPeta, nepotesil jsi me 
Ted se budu muset podivat, kde jsem udelal chybu Pritom jsem mel takovou radost, jak "hezky" mi to vyslo.
Prekvapilo me, jak je ten prepocet udelany profesionaly jednoduchy. 
Do te doby bych se vsadil, ze to bez goniometricke funkce nepujde.
Takze uz jsem "chybu"nasel! Problem byl v tom, ze jsem predtim nikdy stereograficke zobrazeni nevidel, takze jsem vychazel z obrazku, kde je promitaci rovina "vodorovne s jiznim polem". Podle tech vypoctu vyse to ale vypada, ze rovina je "v urovni rovniku", takze u meho vypoctu to jen znamenalo podelit jednu stranu trojuhelniku dvema, prepocitat uhly (θ= 51° ) a take mi vyslo [4/9 ; 4/9; 7/9].
Kdybych to ale jeste nekdy pocital, tak pouziji mnohem lepsi prevodni vztahy profeionalnich matematiku
My se v tom trošku ztrácíme. Byl by někdo tak hodný a napsal nám to do Wordu s kroky jak postupoval: jasně, přehledně a výstižně. Možná, že otravujeme, ale rádi bychom to pochopili, jak jste došli k výsledku. Emai: IANKYS@centrum.cz
Děkuji
Proste pouzijte ty prepocetni vztahy z toho PDF, prekreslete obrazek od uzivatele PetaPeta a je to.
Je to jako kdyz clovek prepocitava rekneme ty sfericke souradnice na kartezske - bud muze pouzit prevodni vzorce sesbirane v matematickych tabulkach (skriptech, poznamek z prednasek) a pouzit je bez chapani pozadi nebo se snazit si je sam odvodit a dojit k uplne tomu samemu vysledku.
Kolik lidi, proc se koreny kvadraticke rovnice pocitaji tak, jak se pocitaji? Naproste minimum lidi. Vsichni ostatni pouziji znamy vzorec na vypocet.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.