Dobrý večer, opět prosím o radu:
1+ tg x * tg x / 1+ cotg x =
tg x * cotg x + tg ^ 2 x / tg x * cotg x + cotg x =
Kdybych vytkl v čitateli tg x, ve jmenovateli cotg x, nic by to nepřineslo. Zkoušel jsem to i jinak, ale vůbec mně to nejde.
Děkuji.
0x
Z vašeho zápisu není zřejmé, jaké je zadání.
cotg(x) = 1/tg(x), takže tg(x) ⋅ cotg(x) = 1
Vy jste zadal:
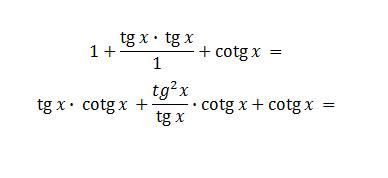
Takže jste to měl zapsat takto: [(1 + tg x)/(1 + cotg x)]*tg x =
A takle se to může upravit:
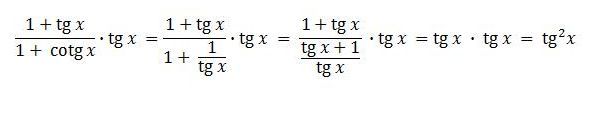
Děkuji mockrát, já zde mám ještě pár takových příkladů, u kterých se plácám a nic kloudného nevymyslím. Když budete tak hodný, prosím
Napíšu to znovu, protože to vypadá jako rovnice:
(sin x) / (1-cos x) + (1+cos x) / (sin x)
Děkuji za pomoc.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.