Dobrý den, nevíte někdo, jak vypočítat z jaké vzdálenosti lze vidět špičku věže, která je vysoká 96.3 m(na rovném terénu)?
Vůbec mě nenapadá jak to spočítat.
Děkuji
Neumělka ![]()
4x
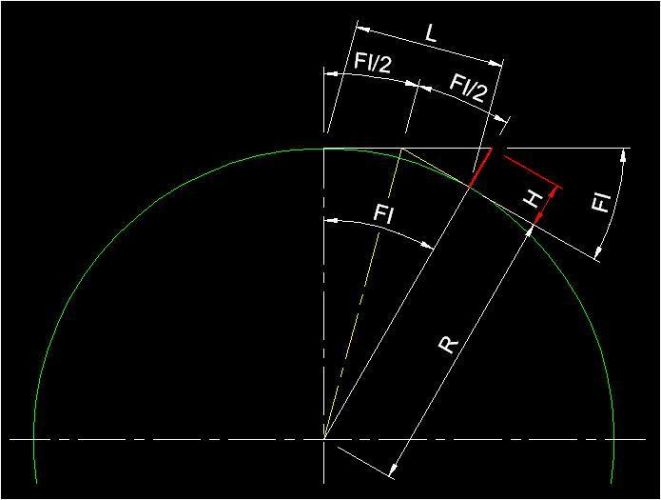
mrkněte se na obrázek, namaloval jsem vám schéma, jak by mělo vypadat. Červeně nakreslená je vaše věž. Problém je ten že vzdálenost L kterou počítáte, je v obloukové míře. Takže nejdříve se musíte prokousat k úhlu FI. Není to zase tak složité, protože uhel FI se ve schematu objevuje dvakrát.
Jestli ale chodíte na VŠ, pak to vypadá na výpočet delší odvěsny pravoúhlého trojúhelníku, ke které se dostanete přes limitu poloměru země R, který je 62305x větší než vaše výška H a tak můžeme říct, že se blíží nekonečnu. Výška trojúhelníka je vašich 96.3 m, délka přepony = délka odvěsny.
Co na to říkáte Neumělko? Jak jsem povídal, není to zase tak složité, že ne? ![]()
No a douška na závěr, raději tuto úlohu nepočítejte jako délku tečny, jak vám tady napovídají nebo dostanete v nejlepším případě čtverku.
Přibližný vzorec pro vzdálenost pravého horizontu je d = sqrt(13h), kde d je vzdálenost v kilometrech a h je výška v metrech. (O něco přesnější je vzorec d = sqrt (2Rh), kde R je poloměrzemě v kilometrech. Prostě délka úseku tečny, vedené z toho bodu ve výšce h k Zemi, mezi bodem pozorovatele a bodem dotyku.)
doplněno 25.10.15 17:23:
Oprava nepřesnosti: v tom "přesnějším" vzorci mí buď být vzdálenost v kilometrech, nebo ten vzorec má být
d = sqrt (2Rh/1000).
0x
Figurek nakreslil moc pěkný obrázek, a jak říká, ta hledaná vzdálenost (braná po povrchu země, můžeme říci "vzdálenost obzoru") je rovna R.F1 (F1 v obloukové míře, jinak bychom psali R . arc F1), kde R je poloměr země. Takže bych jen doplnil výpočet toho úhlu. Když označím dejme tomu t přímou vzdálenost obzoru od vrcholu věže (není to v pravém slova smyslu délka tečny, protože tečna je vlastně přímka a jako taková má nekonečnou délku, ale někdy se to tak říká), tak tuto vzdálenost spočteme Pythagorovy věty a pak spočteme například tangentu úhlu T1 : tg T1 = t/R. No a pak , chceme-li počítat přesně, spočteme T1 jako inverzní funkci k tangentě. Nicméně, jelikož t je proti R zanedbatelné, tak můžeme pokládat tg T1 za rovnu T1 a vzdáletnost obzoru pokládat za rovnu délce t úseku tečny, vedené k Zemi z vrcholu rozhledny.
Samozřejmě, je to zjednodušení, ale první zjednodušení je v tom, že Země není úplně přesná koule, takže vlastně nemá poloměr; přestu v podobných úlohách ji za kouli považujeme a R nějak definujeme (ve škole jsme se učili, že R je šest tisíc třista sedmdesát osm kilometů, mnemotechnicky šetři se osle).
doplněno 08.10.12 09:11:A ještě poznámka na závěr: tohle byl výpočet vzdálenosti obzoru při pohledu z vřšku věže, nebo chcete-li. vzdálenos, ze které by tu špičku viděl slimák. Pozorovatel má ovšem také nějakou výšku; pokud bychom ji chtěli zohlednit, museli bychom podobný výpočet provést i pro něj a výsledky sečíst. (Drobná potíž je v tom, že nevíme, jak je pzorovatel vysoký. Bude určitý rozdíl, jestli bude esedět ve Velorexu, půjde pěšky nebo pojede na koni. Tak velký rozdíl to zase nebude, ale upozorňuji na něj.)
doplněno 08.10.12 11:12:Orientačně, vzdálenost obzoru vyjde něco přes 35 km; vzdálenost obzoru od pozorovatele vysokéhometr sedmdesát je necelých pět kilometrů.
Teď ještě pozor na to, aby se věž nacházela v terénu, který je rovný v okruhu nějakých těch cca 40 kiáků a nezalsněný a bez vysoké zástavby.
0x
Tak co, neumělko, bylo to to, co jste potřebovala?
Jinak, ono mi to nedá, abych se nezeptal Figurka, jak to myslel s tím druhým postupem. Dlouho jsem o tom přemýšlel, ale prostě z toho, co napsal, nechápu, co měl na mysli.Jistě, výška věže je zanedbatelná vůči poloměru země, ale jeho popis je prostě nesrozumitelný. (Kdyby byl ještě tak laskav a vysvětlil mi, proč si myslí, že za výpočet via délka tečny by tazatelka dostala nanejvýš 4, byl bych rád, já totiž nevím, jak by se to dalo počítat bez toho, aby v tom výpočtu nebyl výpočet délky tečny (přesněji vzdálenost vrcholu věže ot bodu dotyku tečny) alespoň implicitně skryt.
doplněno 25.10.15 16:37:
Ad @figurek: To nebyly řečnické otázky. Ale figurek to asi neumí vysvětli, jinak bý nenapsal takovou nesmyslnou odpověď, ze které se nedá nic vypočítat. .
0x
Neumelko podla mna navštevuje iba 7.tr základnej školy a ked preberali pytagorovú vetu tak,nebola v škole .Inak by vedela ,že tieto 3 body tvoria pravouhlý trojuholník - stred zeme-vrchol veže a bod dotyčnice idúcej z vrcholu veže na oko slimáka. Pravý uhol je u slimáka .Prepona má dlžku 6378,0963km =/polomer zeme + výška veže / jedna odvesna je 6378km a tá vypočitaná je 35,0485km.Výška postavy pozorovateľa sa neberie v úvahu!
0x
Tady máte výpočet. Pokud si sestavíte v Exelu, dole uvedený vzorec, postačí jen dosazovat údaje H1 a H2. Výsledek L1, L2 a L se automaticky vypočte Já jsem se pokusil do uvedené tabulky dosadit Vaše hodnoty i když jednu hodnotu H1 nebo H2 neuvádíte. Dosadil jsem H1= běžná výška člověka.
-miro
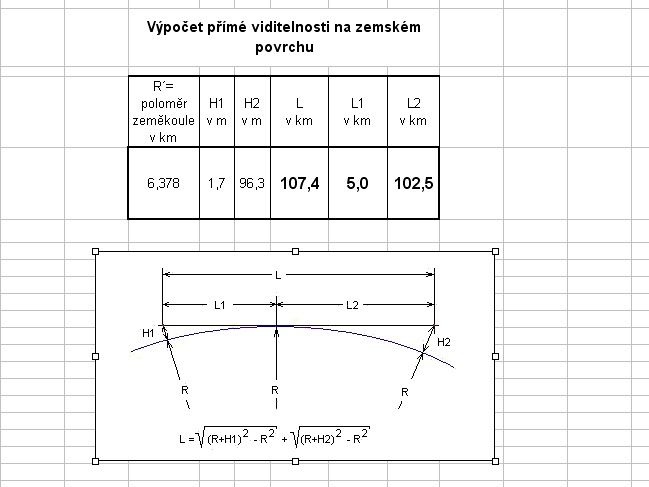
Obrázek i vzorec je OK, ale někde jste musel udělat chybu v dosazení. Když odhlédneme od toho, co psáno výše (ono, po pravdě, výše je psáno mnoho nesmyslů a ještě ohodnocených čtyřmi body), tak nabízím jako kontrolní zdroj Wikipedii: . Vzdálenost pravého horizontu při výšce oka 1,70 m činí asi 4,7 km, při výšce 100 m asi 36 km.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.