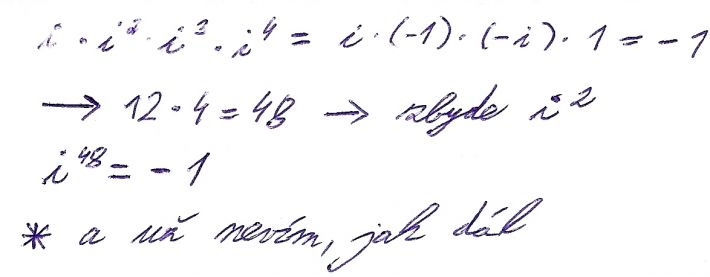Zdravím všechny,
potřebovala bych nastínit postup těchto příkladů. Znám onu řadu, např. že i^5 je i. Ale tohle mi moc nepomůže. Potřebovala bych to vysvětlit úplně laicky, něco jako pro úplného blbce, abych to pochopila. Díky moc všem. Anzionka.
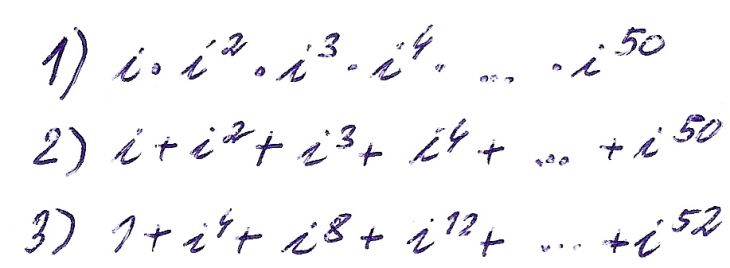
2x
Ono to jde různě. Například u příkladů 2 a 3 se jedná o součet (konečné) geometrické řady s kvocientem i, resp. i na čtvrtou, a na to jsou vzorečky. A po jejich aplikaci pak to mohu upravit podle dzordze. A příklad 1 - to je součin? Tak tam zase sečtu exponenty, které tvoří, pro změnu, aritmetickou řadu. Bude to stačit takhle?
doplněno 17.06.12 20:46:Ale vůbec neříkám, že tohle je nejjednoduěěí, zamyslel bych se nad tím, co píše dzordz, tohle uvádím jako alternativu.
Takže u prvního příkladu ty exponenty musím sečíst? A jak se mám jako všechny sečíst až do padesáti? Ze začátku je to lehké - i^1*i^2=i^3 -> i^3*i^4=i^7 ... A jak mám pokračovat až do padesáti? Není na to nějaký fígl? Druhý a třetí příklad - to mám jako nahrazovat íčka podle pravidel, tak to mi zabere spoustu času ... Možná, že jsem to nepochopila. Chtělo by to ještě jednoduší vysvětlení. Ale i přesto děkuji za odpověd/i. ![]()
PS: Teď mně napadlo, nedalo by se to sčítání (konkrétně ten druhý příklad) udělat tak, že spočítám, kolik je od i do i^4 a pak zjistit, kolikrát to tam v té padesátce je? 50/4= 12,5? To je nějaké divné ... To asi ne.
Tak se mi to zavřelo po dlouhám psaní. to je osud,
S tím prvním příkladem: ano a ano: sčítáme až do padesáti (jen pozor, v té úvaze je překlep. První součty jsou 1. 1+2=3. 1+2+3 = 6 atd). a je na to fígl. Součet 1+2+3+...+50 je aritmeticá řada nebo,.chcete-li součet aritmetické posloupnosti a na to je vzoreček.
1+2+3+...+n = n*(n+1)/2, což pro n = 50 dává 3050, No a ta ředa umocněných i je, jak víme i,-1,-i.1 a pak se to opakuje, čili stačí výsledek vydělit čtyřmi a i umocnit pouze na zbytek.
Tak a teď to radši odešlu, než se mi to ztratí.
doplněno 18.06.12 10:01:Pospíchal jsem o odeslal to předčasně. Když se podíváte na použitý vzorec, vidíte, že 3050 ještě není hledaný součet, ještě je třeba ho vydělit dvěma, takže hledaný výsledek je 1275. Dále už to platí.
Bi a tato myšlenka, kolik čtveřic je do padesáti, je výborná, jen je to třeba interpratovat tak, že je jich tam padosát celých, ty snaadno sčteme, no a ty dvě co tvořej půlku čtveřice (zase dělění se zbytkem) vyřešíme extra
Díky za rady, mrknu se na to, zkusím to spočítat a dám sem potom výsledky, abych věděla, jestli to mám dobře. Anzionka.
Začátek dobrý. Každá skopina čtyž mocnin i dá tedy -1. Těch prvních dvanáct skupin dá tedy (-1)^12 = 1 (sudá mocnina mínus jedné,
takže i*i^2*...*i^48 = 1 (ne i^48, jak píšete, myslíte to dobře ale není to dobrý zápis. No a zbývá i^49*i^50 = i*i² (začínáme znovu od začátku díky periodicitěú = -i.
Tím druhým postupem, který jsem navrhl výše, to vyjde taky, k tomu se vrátím po snídani.
doplněno 18.06.12 09:59:Ten druhý postup: tam mám chybu, respektive nedopočítal jsem to. vyšlo mi 50*51 = 3050, ale když se podíváte na vzorec, musíme to ještě dělit dvema, takže uvažovaný součin je roven i^1275. (já to ještě doplním do příslušné odpovědi, aby bylo jasno.) Tak a teč budeme dělit se zbytkam:
1275:4 =318, zbytek je 3
takže díky periodicitě
i*i^2*...*i^50 = i^1275 = i^3 = -i.
Ono všechny uvedené úlohy lze řešit různě (minimálně dvěma způsoby), ale nakonec vždy budeme dělit čtiřmi se zbytkem, nebo, chcete-li to vznešené, počítat s kongruencemi mdulo 4. Zvládnete ty dalšíúlohy, nebo je mám taky rozebrat podrobněji? Ideje jsou stejné,ale nějaké rozdíly tam pochopitelně jsou.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.