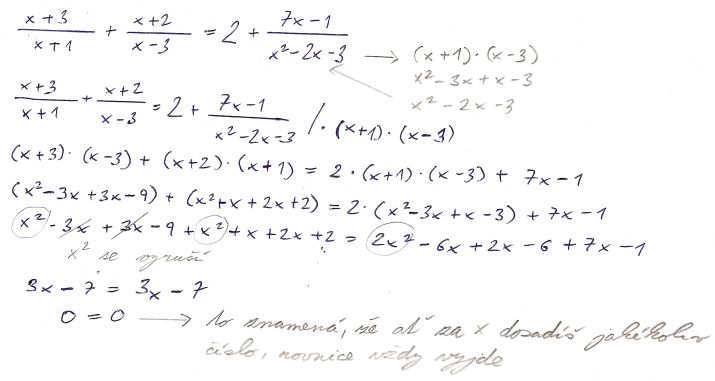Dobry den, jsem zoufala... v pondeli piseme cvrtletku z matiky a ja to vubec nechapu... uz jsem to delali asi pred 2 lety ale ted se to opakuje ja vubec nevim... nastinil byste nekdo prosim reseni zakrouzkovanych prikladu? dekuji moc
doplněno 02.06.12 17:02:mozna ze se to bude nekomu zdat lehoucke ale ja jsem na matiku vazne blbec tak se nezlobte...

4x
Noo, něco bych tu do matematiky měla...sem to propočítala...![]()
12) První rovnici celou vynásobíte (x+1).(x-3) - protože (x+1).(x-3) = x2 - 2x - 3
Tím si odstraníte zlomek a úpravy jsou pak zřejmé
13) Druhou rovnici násobíte (2x + 5)2 . (2x + 1)2 - tím se opět zbavíte zlomků a úpravy jsou pak zřejmé.
x2 je x na druhou - tj. červená dvojka je exponent.
Na závěr nezapomeňte, podmínku, že ve jmenovateli nesmí být výraz rovný nule! Protože nulou nelze dělit.
Ostatní jsou podobné. Jen bych doporučil ty podmínky nenulovosti jmenovatele stanovit předem, je to takové čistší (i když tady je to jedno). A taky: nelekni se, že ze začátku to bude vypadat jako kvadratická rovnice, ale ono členy s x² se vyruší.
Nepočítala jsem to, ale určitě se to vyruší, protože máte na začátku příkladů napsáno lineární rovnice, ne kvadratické. Tudíž tam nemůže být x².
Kdyby se nevyrušilo, tak bychom měli smůlu, byla by to kvadratická rovnice. Ale ono se vyruší, anzionka je o tom z dobrého důvodu přesvědčena a já to mohu potvrdit i proto, že jsem to počítal; ono je to celkem dost vidět , ani jsem to nemusel počítat do konce. Takže ten dotaz "cobym, kdyby " je předčasný, chce to nejprve zkusit (a kdyby to přeci nevyšlo, ptát se, zda jsem udělal chybu já nebo autor zadání; i to by bylo možné).
Doplním: jakékoli číslo kromě x = _1 a x = 3. To jsou právě ty podmínky, a taky důvod, proč je stanovovat předem; v průběhu výpočtu se jejich potřeba jaksi vytrácí.
Nemáš zač děkovat. Všechny příklady si zkus spočítat, tím si to nejlépe procvičíš. Kdybys narazila na nějaký problém, tak napiš. Pokud by byl problém, hoď sem řešený příklad najdeme chybu nebo pomůžeme s řešením. Anzionka. ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.