zdravím, ve škole mám vést diskuzi na otázku: čím se liší komplexní čísla od čísel reálných? něco jsem si našel, ale potřeboval bych pomoci jelikož moc rozumu jsem z toho nepobral, ocenil bych kdyby mi někdo napsal co je důležité a osvětlit ty důkazy a definice, děkuji
3x
Koukám, že jsem v tom předchozím příspěvku nadělal spoustu překlepů. Inu, festina lente!
Ale k věci. Začal bych reálnými čísly. Ta lze zobrazit na číselné ose pomocí orientovaných vzdáleností a ztotožnit s body této osy, vpravo od počátku kladná čísla, vlevo záporná. Lze je sčítat, odčítat, násobit a nenulovým číslem lze i dělit. (Mají ještě spoustu dalších zajímavých vlastností, ale tím se zabývat nebudu, myslím, že reálná čísla lze pokládat za dostatečně známá.)
Reálná čísla mají ale jednu nevýhodu: v oboru reálných čísel nelze vždy řešit algebraické rovnice, dokonce ani kvadratické ne. Nevyřešíte ani tak jednoduchu rovnici, jako je x² + 1 = 0, protože byste museli odmocňovat záporné číslo. A tak se matematici rozhodli, tento neexistující kořen si jaksi "vymyslet", a zavedli "ideální prvek " (ideální ne ve smyslu obzvlášť dokonalý, ale ve smyslu "myšlený, v idei, v představách existující, imaginární), označili ho i a definovali ho vlastností, že i² = _ 1, tedy že řeší tu protivnou rovnici, no a aby se s ním dalo počítat, přidali spolu s ním k eálným číslům i všechny možné kombinace i s realnými čísly, tedy všechna "čísla" tvaru w = a + i b, kde a, b jsou čísla reálná, a vzniklý soubor, množinu, nazvali oborem reálných čísel. Čislu a pak říkáme reálná část čísla w a píšeme například a = Re(w), číslo b = Im (w) je jeho imaginární část.
Pokud vám je takový neexistující prvek proti srsti, není se co divit, nejste v historii matematiky první ani poslední. Možná vás s tím smíří, když si uvědomíte, že taková ta ležatá osmička, kterou označujete "číslo" nekonečno, je taky jen ideální prvek. žádné nekonečno ve skutečnosti neexistuje,. A nakonec i všechna čísla jsou ideální prvky. Viděl jste někdy "jedna" an sich? Mohl jste vidět jeden talíř, jednu lžíci, jednu vydličku, jeden nůž, můžete potkat jednoho kartagince, v zrcadle vidět jednoho traba, ale co je to "jeden" bez dalšího určení? Anebo na to můžeme jít jinak, pro začátek zapomenout na symbol i, definovat komplexní číslo w =[a,b] jako dvojici reálných čísel, dvojice [a,0] prohlásit za reálná čísla a dvojici [01] nazvat i; zmiňuji se o tom proto že nevylučuji, že takhle jste komplexní čísla definovali ve škole; poku ano, museli jste si k tomu říci, jak se takové dvojice sčítají, násobí a tak a následně touto cestou teorii komplexních čísel vybudovat. Je-li tomu tak a je vám v této metodě něco nejasného, napište, ale jí prozatím se budu držet toho, co jsem zatím napsal, a v dodatku k této odpovědi se rozepíšu k pravidlům a důkazům, o která vám jde. ALe v podstatě můžete ten dosavadní text brát jako doplnění odpovědi hm, vrátit se k ní a pro podrobnosti jít dle jeho rady do wikipedie.
doplněno 09.09.12 18:40:Tak teď k počítání. Řekl jsem, že komplexní čísla jsou čísla (výrazy) tvaru w = a + i b, kde a,b jsou reálná čísla, a je reálná, b imagonární složka čísla w, a i je "odmocnina z mínus jedné", tedy i² = _ 1. S těmito čísly se počítá normálně jako s reáknými, jen bereme na vědomí ten základní vztah i² = _ 1, takže:
(a±ib) + (c±id) = (a±c) +(b±d) i
(a+ib) *(c+id) = (ac -bd) +(ad +bc)i (roznásobíme a upravíme, to zvládněš)
Násobení je malinko složitější, zejména co do zápisu s omezenámi možnostmi psaní vzorečků, tak sem vložím obrázek.
Takovémuto tvaru se říká algebraický tvar komplexního čísla, a jak vidět, výsledky všech algebraických operací na tento tvar snadno převedeme, i když třeba právě to dělení na první pohled vypadá problematicky. Je-li b = 0, jde o číslo reálné, pro a = 0 mluvíme o čísle ryze imaginárním.
Dále, tak jako reálná čísla lze znázornit na číselné ose, komplexní čísla lze znázornit v rovině, kde zavedeme kartézské souřadnice a jako první souřadnici vezmeme reálnou část, jako druhou komplexní část. Číslo w pak znázorníme jako bod [a,b] o těchto souřadnicích, nebo, což je někdy výhodnější, jako vektor (a,b) o těchto souřadnicích, nebo, chcete-li jako průvodič toho bodu (vektor, šipku, jehož počátek leží v počátku souřadné soustavy a koncový bod je ten bod [a,b]. (Proč je to výhodnější? No třeba proto, že součtu dvou čísel odpovídá vektorový součet těchto obrazů. Se součinem je to složitější, ale i tam jsou určité vztahy. To už ale spíš nepatří k těm úplným základům.) Další základní pojmy jsou: absolutní hodnota, což je v tomto geometrickém znázornění vzdálenost bodu [a,b] od počátku, čili |w| = sqrt (a² + b²). amplituda neboli argument (to jsou dva používané názvy téhož), kterou nejlépe popíšeme jako orientovaný úhel α, který svírá vektor (a,b) s reálnou osou (amplituda tedy není jednoznašně určena, s úhlem α, tomůže být i ůhel α + 2π atd; prostě amplituda je uršena až na periodu 2π). No a s tím souvisí goniometrický tvar komplexního čísla: w = |w|(cos α + i sinα).
Komlexní čísla mají ještě ředu dalších důležitých vllastností, ale jako základ bych vzal toto, ostatní si najdete v učebnici nebo třeba ve Wikipedii, nebi i v jinén zdroji, google poraí, Snad jen jedna drobná zajímavost: číslo 0 je sice reálné, ale zároveň je paradoxně ryze imeginární.
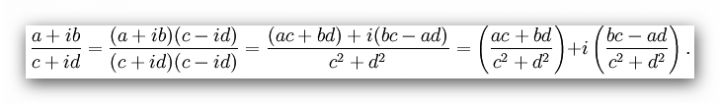
2x
Komlexní čísla mají imaginární složku. Resp. mají reálnou a imaginární složku, ta reálná je reálné číslo, imaginární část je to, co mají proti reálným číslům navíc. Je-li imaginární složka nulová, jedná se vlastně o normální reálné číslo. Reálná čísla jsou podmnožinou komlexních čísel. Na podrobnější popis se podívej třeba na wikipedii.
1x
To je v zásadě pravda, ale postrácám zdůracnění toho podstarného, totiž že v komplexních číslecjh existují odmocniny ze záporných čísel, speciálně mezi nimi je "imaginární jednotka" označovaná obvykle i, kerá má tu vlastnost, že i² = -1. Obecné komplexní číslo pak má tvar a + ib, kde a je ta výše zmiňovaná reálná složka a b imaginární složka.
Teď jdu pryč, pokud to někdo nedoplní, napíšu víc odpoledne.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.