Zdravím,
mám jeden takový příklad, u něhož nevím postup, nemohl by mi to někdo nastínit?
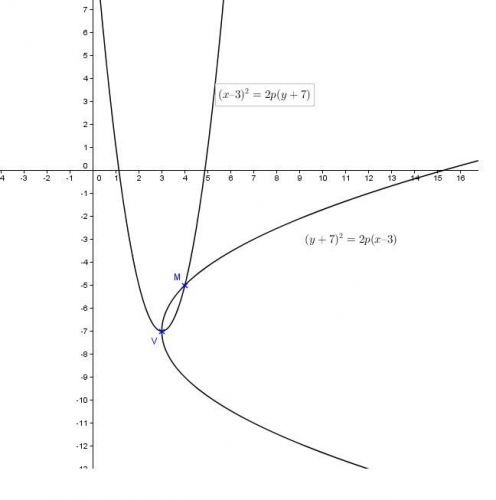
Napište rovnici paraboly, která má vrchol V (3, -7), prochází bodem M (4, -5), a jejíž osa je rovnoběžná se:
1) souřadnicovou osou x
2) souřadnicovou osou y
Mám pár nápadů, jako, že abych napsala rovnici, musím zjistit p, tj. vzdálenost ohniska od řídící přímky, ale to je asi tak všechno, co mě napadá. Díky moc za pomoc. ![]()
2x
Rovnice paraboly s vrcholem v bodě V[m,n] je (x-m)² = 2p(y-n) (osa rovnoběžná s osou y a parabola "otevřená nahoru), ostatní varianty jsou podobné ' aristoteles.cz/... V této rovnici neznáme jedině p. Takže stačí dosadit do té rovnice bod M a p vypočítat (musí vyjít kladné).
Takže, pokud má být parabola rovnoběžná s osou x, tak bude rce ve tvaru (y-m)² = 2p (x-n). Dosadím tam za m a n souřadnice vrcholů a dostanu (y+7)² = 2p (x-3). Poté dosadím za y a x a budu mít (-5+7)² = 2p (4-3) -> (-8)² = 2p (11) -> (-2)² = 2p* -> 4 = 2p. Takže se p bude rovnat 2. Rovnice tedy bude vypadat (y+7)² = 4 (x-3). Mám to správně?
doplněno 30.05.12 17:10:Do postupu výpočtu se dostala chyba: (-5+7)² = 2p (4-3) -> (-2)² = 2p -> 4 = 2p
Takhle to bude.
0x
Protože již si houbec pamatuji jedině snad vzorec vrcholové paraboly x² = 2py nebo taky x² = -2py pokud má být rovnoběžná s osou x, tak bych si udělal transformaci na souřadnice vrcholu [0,0] a bodu M [1,2] a dosazením těchto hodnot do vzorce by snad již neměl být problém vypočítat paramer "p". Totéž pro osu y když y² = 2px či y² = -2px. No a výslednou rovnici by již neměl být problém převést na požadovaný tvar.
Můžu ještě jeden dotaz, mám rovnici hyperboly ve tvaru 9x²-16y²+36x+32y+164=0 a nějak mi vychází záporné číslo na levé straně rovnice, připadá mi, že to není rovnice hyberboly, i když je uvedena v učebnici. Provedla jsem následující úpravy:
* 9(x²+4x)-16(y²-2y) = -164
* 9(x+2)²-16(y-1)² = -164+36+16
* 9(x+2)²-16(y-1)² = -112 -> TOTO JE VELMI DIVNÉ, ŽE JE TAM ZÁPORNÉ ČÍSLO
Nevíte, kde mám chybu nebo to mají špatně v učebnici?
No obecná rovnice hyperboly je to určitě. Ale myslím si že v tom pokusu převést na středový tvar je chyba
9(x²+4x)-16(y²-2y) = -164
9(x²+4x+4-4) -16(y²-2y+1-1) =-164
9(x+2)²-16(y-1)² -36+16=-164
9(x+2)²-16(y-1)² =-164+36-16
9(x+2)²-16(y-1)² =-144
doplněno 30.05.12 20:12:
Doplním. Když obě strany rovnice vydělíme -144 máme na levé straně koeficienty v mocninách celých čísel a dostaneme středový tvar hyperboly jejíž hlavní osa je rovnoběžná s osou "y"
Ale i přesto, že jste mi odstranil chybu, na pravé straně rovnice je pořád záporné číslo. Nevím, zda tam může být ... Řekla bych, že když je tam záporné číslo, tak je to jaksi divné.
Je doplněno
doplněno 30.05.12 20:24:Nechtělo se mi mastit ty závorky a lomítka, když zlomková čára nejde tak snad výsledek bude
(y-1)²/3² - (x+2)²/4² = 1
Promiňte, ale jaksi to pořád nechápu. Mohl byste napsat rovnici ve středovém tvaru po úpravě, kterou popisujete?
doplněno 30.05.12 20:27:Tak už to chápu, díky. Takže může klidně na pravéstraně být záporné znaménko? Jsem zvyklá, že u kružnice nemohlo, jinak by to nebyla kružnice.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.