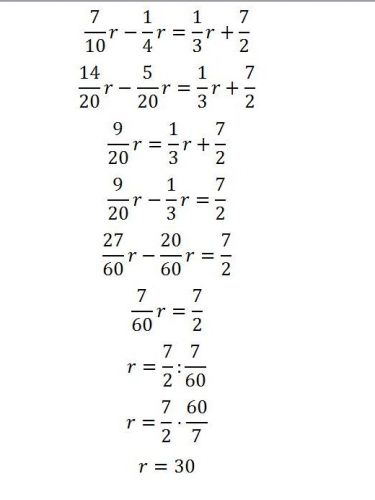Nejste přihlášen/a.
Dobrý den chtěla bych se zeptat jak řešit lineární rovnice se zlomky. Písemnou práci jsme psali ve středu a opravku píši teď v pondělí. Byli byste mi ji ochotni vysvětlit? Předem děkuji za vysvětlení ![]()
![]()
2x
Co máte na mysli označením "lineární rovnice se zlomky"? Trefil se Jirbar? Já to nevylučuji, na druhou stranu to, nač odkazuje, nejslou lineární rovnice. Co kdybyste sem dal aspoň jeden příklad, ať víme, o čem se bavíme, a taky ať je na čem začít vysvětlovat.
Taky jsem si kladl otázku co tím myslí. S nevětší pravděpodobností s neznámou ve jmenovateli. Článek jsem moc nestudoval, jen mi stačilo, že v nadpisu je Lineární rovnice.
No ono je to o lineárních rovnicích, a je to i o takových rovnicích, kteé mají neznámou ve jmenovateli a dají se na "klasickou" lineární rovnici převést, takže to může být (a nejspíš je) to, co tazatel chce. Ale někdo tím označuje rovnice, které jsou lineární v klasickém smyslu, ale mají zkoeficienty ve tvaru zlomku, Takže jsem položil tento dotaz pro upřesnění.
No tak třeba mám v sešitu 7 desetin a za tím je r (OMLOUVÁM SE ALE NEVÍM JA SE PÍŠÍ ZLOMKY :D ) mínus 1 čtvrtina r = 1 třetina r plus 7 polovin
Krásné na matematice je mimo jiné to, že tento postup je správý, ale ne jediný. Jiný postup je takový, že celou rovnici vynásobíme šedesáti (což je společný jmenovatel všech těch zlomků) a hle - dostaneme rovnici s celočíselnými koeficienty
42 r _ 15 r = 20 r + 210
Anebo, když se mi nechce předem počítat společného jmenovatele, vynásobím tu rovnici deseti, čímž zmizí ten první zlomek (ze sedmi desetin se stane sedm) a k mé velké radosti i ten poslední ... místo 7/5 dostaneme 35. Stále tam budou ještě poloviny (da druhém místě se mírot 1/4 objeví 5/2), tak to vynýsobím pdvěma, no a nakonec třemi (čili celkem šedesáti, jen tak bokem jsem toho nejmenšího společného jmenovatele určil.
No a na závěr to řeším jako lineární rovnici s celočíselnými koeficienty.
(Viz též aristoteles.cz/... )
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.