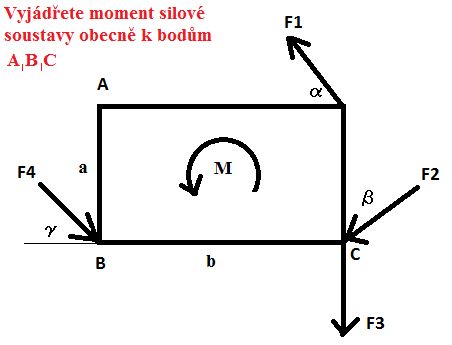
Nevím si rady s tímto příkladem, víte někdo? Předem díky za odpovědi.
1x
Moment je rameno krát síla kolmá k tomuto rameni. Musíme uvažovat směr, takže některá z těch sil múže být vůči jiné síle záporná. Protože síla je dána obecně, musíme ji rozložit na složku kolmou na rameno (ta nás zajímá) a na složku rovnoběžnou s ramenem.
doplněno 04.03.13 22:34:Např. K bodu "B" je moment síly F3 záporný a jeho velikost je M = b*(-F3)
0x
Síly F1, F2 a F4 rozložíš do vodorovného a svislého směru. Moment od síly k urřitému bodu je síla krát rameno. Pak už zbýva jen si zvolit kladný směr momentu a sečíst všechny momenty, které k danáme bodu působí.
doplněno 04.03.13 22:31: zase pozdě ![]()
0x
Moment se počítá taky tak, že se plohový vektor síly (tedy průvodičvektor působiště síly) vynásobí příslušnou silou vektorově. Vektorový součin dvou vektorů X = (x1,x2,x3) a Y = (y1,y2,y3) se spočítá tak, že spočteme "determinant", jehož prví řádek je tvořen vektory i, j, k (vektory báze, souřädnámy vektory) a druhé dva řádky jsou tvořeny vektory X, Y (v tomto pořadí). V souřadnicích:
X × Y = (x2*y3 _ x3*y2, x3*y1 _x1*y3, x1*y2_y1*x2)
Názvem "rameno síly" obvykle označujeme kolmou vzdálenost přímky, ve kterém síla působí, od bodu, ke kterému moment počítáme. Ten popis výpočtu v předchozích dvou příspěvcích vcelku odpovídá, jen terminologicky je to trochu zmatené, mimo jiné i proto, že poněkud směšuje sílu jako takovou, což je vektor (veličina daná velikostí a směrem), a velikost síly, což je skalár. Takže ono je sice dost zřejmé, co tyto příspěvky myslí pod pojmy ve vyjádření "rameno krát síla", ale formulace je to zkratková a tím pomněkud nepřesná.
doplněno 05.03.13 15:40:
Prosím promiňte překlepy, snad je to srozumitelné. Kdyby to někomu srozumitelné nebylo, nechť se ozve a já to přepíšu pozorněji.
doplněno 05.03.13 15:55:A ještě doplním, že jelikož ty vektory , jejichž momenty počítáme, jsou komplanární a všechny leží v rovině kolmé ke třetí ose souřadné (k vektoru k ) pak x2*y3 _ x3*y2 = x3*y1 _x1*y3 = 0 a moment (včetně znaménka) je dán složkou x1*y2_y1*x2, Pokud je tato složka kladná, znamená to, že se moment snaží rovinu i.j otáčet proti směru hodinových ručiček (z hlediska pozorovatele, který na ní stojí orientován ve smylu vektoru k (pravidlo pravé ruky).
0x
Takze treba pro bod A bude prispevek od F4: sila = F4 * cos γ (coz je slozka sily F4 kolma na spojnici mista ucinku a bodu otaceni, tj. bodu A), vzdalenost = a; prispevek od F1 bude: vzdalenost = b; velikost = F1 * cos α ; prispevek od F2 bude: vzdalenost = sqrt (a^2 + b^2); velikost = minus F2 * cos (β + 45° - 90° ) (minus proto, ze sila pusobi v protismeru); analogicky pro F3 a pak to cele znovu pro body B a C.
Snad jsem to zadani pochopil spravne.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.