Nejste přihlášen/a.
Dobrý den, potřeboval bych poradit jak na postup tohoto příkladu, jelikož mám přijímačky v pondělí a úterý , nemám na to moc času.
Zkoušel jsem to vyřešit, ale špatně.. Děkuji za odpověď ![]()
Zadání: a) Do kružnice k je vepsaná tětiva BC. Na kružnici umístěte bod A tak, aby vznikl rovnoramenný trojúhelník ABC se základnou AB.
Jakou délku má základna AB? Jakou velikost má výška na stranu BC?
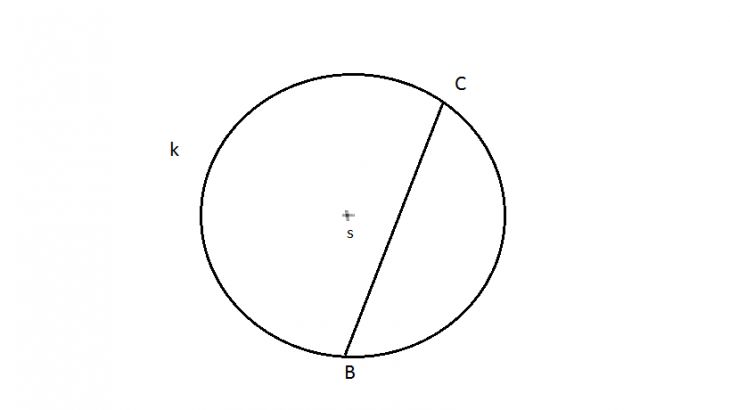
Zabodni kružítko do bodu C, vezmi si do něj délku strany BC a opiš kružnici. V bodě kde se protne s kružnicí k je bod A. Jedna strana musí být stejně dlouhá (rovnoramenný trojúhelník) a protože základna (přepona) má být AB (delší než zbylá dvě ramena), logicky |AC| = |BC|.
Délka strany |AB| bych řešil přes Pythagorovu větu, ale neuvedl jsi konkrétní rozměry. Tak asi tolik. Doufám, že je můj postup správný. :D ![]()
Výšku na |BC| zjištíš tak, že uděláš tečnu, která projde bodem A a poté uděláš kolmici k BC. ![]()
Ještě dodám, že ta tečna musí být rovnoběžná s |BC|. ![]() Tak asi tolik. :D
Tak asi tolik. :D
Těm doplňkům absolutně nerozumím. Nezaměňujete tečnu se sečnou? A i tak, k čemu mi ta tečna/sečna bude?
0x
Tak konstrukci bodu A popsala jak Tlapka, tak Yeri (i když ta jeho vysvětlující poznámka je mi trochu nejasná - přeponu má pouze pravoúhlý trojúhelník, trojúhelník ABC má ramena a základnu, která nemusí být nutně delší než ramena). Co se týče hledaných délek, záleží na tom, jak přesně zní plné zadání. Pokud je zadání skutečně čistě grafické, tak by nezbylo, než i ty délky řešit graficky . odměřit je, nebo tedy v obrázku vyznačit. (Výška na stranu BC je kolmice spuštěná na tuto stranu z bodu A, kterou jistě umíme zkonstruovat, třeba podle Thaletovy věty.)
Spíš bych asi měli tyto délky spočítat z poloměru r kružnice k a z délky a těžnice BC. Tady skutečně bude základem Pythagorova věta. Začal bych tím, že bych úsečku BS prodloužil, průsečík se stranou AB bych označil třeba S1 a průsečík s kružnicí k třeba C1. Trojúhelník BC1C je pravoúhlý (Thales), dvě strany znám, třetí spočtu (Pythagoras) a pak už budu jen hledat podobné trojúhelníky . Je CBC podobný BC1S1, a také trojkúhelníku, tvořenému stranou AC a hledanou výškou (nepíši to podrobně, jde mi o návod).
doplněno 21.04.12 12:46:Není to samozřejmě jediná možnost, taky by šlo například využít Euklidovy věty a jistě by se našlo mnoho jiných cest.
- Planimetrie, trojúhelník, kružnice vepsaná
- Popis konstrukce kružnice opsané a vepsané
- Příklady s kružnicí
- Vepsaná kružnice
- Rovnice na kružnici
- Planimetrie - příklady
- Kružnice vepsaná
- Geometrie kruižnice
- Poloměr kružnice
- Úhly v trojúhelníku - výpočet
- Planimetrie - úhly
- Kružnice vepsaná, opsaná osmiúhelníku
- Jak narýsovat těžnici
- Apolloniova věta
- Maturitní matematické úlohy
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.