Nejste přihlášen/a.
Dobrý den, vím, že pro vysvětlenou by bylo lepší přiložit obrázek, ale bohužel nejsem doma a nemám po ruce skener ani foťák. Jde mi o to, že pokud chci u prostorového svazku sil vypočítat výslednici - musím si síly rozložit do směrů rovnoběžných s osami souřadného systému (x,y,z). Abych to udělal - musím znát velikost sil a cosiny směrových úhlů k daným osám. Problém je v tom, že v mém zadání jsou nškteré paprsky zadány dvěma úhly. Tj. půdorysným (od osy souř. systému) a výškovým (od půdorysné plochy).
Doufám, že je to alespoň trochu k pochopení. Má otázka zní jak se dopracovat k těm cosinům směrových úhlů. Moc Vám děkuji.
1x
Chtělo by to nakreslit si obrázek. Jde o to, jak určit jednotlivé složky Fx, Fy a Fz. Velikost půdorysné složky určíme pomocí výškového úhlu Fxy = F cos γ. Složku Fx = Fxy cos α, složku Fy = Fxy cos(90° – α ) = Fxy sin α. A složku Fz = F cos (90° – γ ) = F sin γ.
α je úhel mezi osou x a půdorysným průmětem síly F.
γ je úhel mezi silou F a jejím půdorysným průmětem Fxy (výškový úhel).
Geniální - moc mi to pomohlo - děkuji.
Mám však ještě pár nejasností ohledně sil:
1) V rovinném svazku sil mám sílu (výslednici soustavy, kterou mám uvést do rovnováhy dvěma silami. Jedna je zadaná svým paprskem a druhá pouze bodem - působištěm. Výsledkem by měli být velikosti těchto dvou sil a orientace (úhel) té síly co má zadané jenom působiště.
2) V prostoru mám určenou výslednici svazku sil a 3 další síly. Všechny mají působiště v počátku. Úkol je vypočítat úhly, které každá síla svírá s výslednicí.
Ten první bod je mnohem aktuálněší. Kdyby jste našel/a chvilku času a ochoty k napsání podobného obbecného zápisu - budu Vám nesmírně vděčen. Ta první odpověď neměla chybu. Díky
1) Zdali to dobře chápu, tak se jedná o rozložení síly na dvě složky, kdy známe směr jedné složky. Není-li dáno více, než velikost výslednice a směr jedné složky, tak by úloha měla nekonečně mnoho řešení (druhou složku si můžeme libovolně volit). Je zapotřebí dodat další podmínku, buď velikost jedné složky, nebo směr té druhé složky. Znalost působiště nám umožňuje pouze umístění dané síly, popřípadě celého svazku sil.
2) Nevím, jakým způsobem to máte řešit. Já bych úhly počítal pomocí skalárního součinu:
|F|⋅|R|⋅cos α = FxRx + FyRy + FzRz, kde R je výslednice, F jednotlivá síla a α úhel, který svírají.
Myslím, že to chápete dobře. Právě z tohoto důvodu mi to taky nedává smysl. Ve všech vzorových příkladech tohoto typu je jedna síla rovnoběžná s jednou ze souřadnicových os. Čímž odpadá jedna složka síly (je rovna nule) .
Přesné (doslovné) zadání zní takto:
Danou soustavu uveďte do rovnováhy dvěma silami - silou R1 na paprsku AB a silou R2 procházející bodem C. Pro kontrolu budete potřebovat velikost síly R1 a složky, velikost a směrový úhel síly R2.
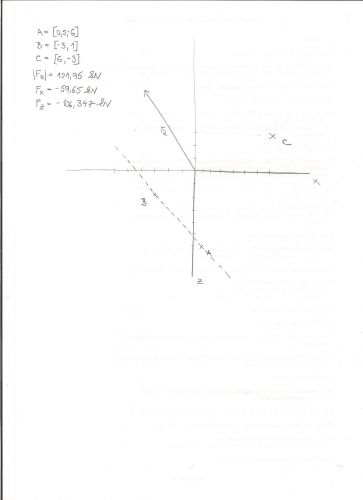
0x
XYZ... jednoduché... Když je něco opačně než do plusu dejte tam mínus a ono to jde, opravdu :D
Nerozumím - to je přece jasné, že síly, které mají záporné znaménko jsou orientovány opačným směrem než na obrázku. Má otázka se ale týká něčeho úplně jiného. Viz. výše.
Každá síla má kladné a záporné hodnoty, záleží na kterou stranu působí a v jakých souřadnicích. Zkuste někdy místo plus dát mínus.
0x
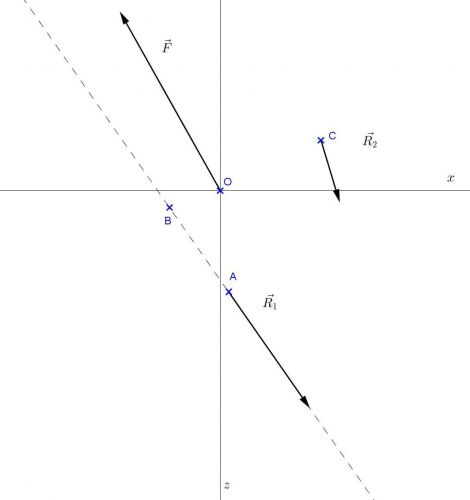
Aby nastala rovnováha, musí platit:
Fx + R1x + R2x = 0
Fz + R1z + R2z = 0
Dále musí platit, že součet momentů sil vzhledem k počátku musí být roven nule:
R1x zA _ R1z xA + R2x zC _ R2z xC = 0
Po dosazení souřadnic bodu A a bodu C :
6 R1x _ 0,5 R1z _ 3 R2x _ 6 R2z = 0
Dále známe směrový úhel síly R1, který můžeme určit pomocí bodů A,B
tgα = (zA _ zB)/(xA _ xB) = 5/3,5 ⇒ α = 55°
R1x = R1cosα = 0,5736 R1
R1z = R1sinα = 0,8192 R1
Nakonec máme 3 rovnice o 3 neznámých:
Fx + 0,5736 R1 + R2x = 0
Fz + 0,8192 R1 + R2z = 0
6.0,5736 R1 _ 0,5.0,8192 R1 _ 3 R2x _ 6 R2z = 0
0,5736 R1 + R2x = 59,65
0,8192 R1 + R2z = 106,347
3,4415 R1 _ 0,4096 R1 _ 3 R2x _ 6 R2z = 0
Řešením v Excelu mi vyšlo: R1 = 84,5 kN, R2x = 11,2 kN, R2z = 37,1 kN
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.