Dobrý den, mám zde opět jednu zapeklitější úlohu. 
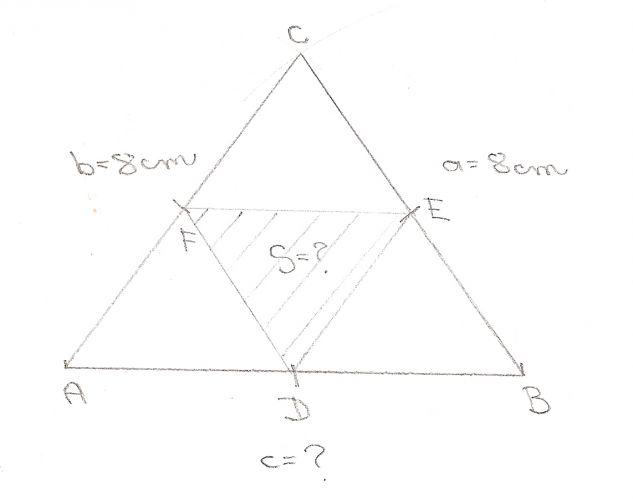
Trojúhelník ABC je rovnoramenný o straně délky 8 cm. Body D, E, F jsou postupně středy stran AB, BC, AC. Vypočtěte obsah trojúhelníku DEF. V jakém poměru je obsah trojúhelníku ABC k obsahu trojúhelníku DEF?
Zvládl jsem ještě tak náčrtek, který přikládám. Nevím, jak dál postupovat. Ze školy znám pouze Pyt. větu a nenapadá mě žádné řešení. Budu moc rád za jakoukoliv pomoc.
Jinak je zcela jasné, že poměr obsahu trojúhelníku ABC k obsahu DEF bude 4 : 1.
2x
Trojúhelník je určen třemi prvky, zde známe pouze dvě strany. Schází zadat ještě jeden prvek. Jak jste narýsoval stranu AB? Jak je dlouhá?
No, to je rpávě ono. Já nevím jak je dlouhá, jestli 3 cm, 5 cm, 6cm nebo kolik. Vím, že ten náčrtek tedy klame a že je špatný, ale jak jinak si ho mám načrtnout a představit? 
Ještě jednou zkontroluji zadání, máme je nadiktované, možná se učitel spletl a trojúhleník je vskutku rovnostranný. Bylo by to logické.
1x
Já teda myslím, že to řešit jde - matně si pamatuji tutéž úlohu ze třeťáku na gymplu - hnusná planimetrie, se kterou měli všichni problémy
ale dalo se to vypočítat...
0x
Co je na tom složitého?
Když spojíš středy stran, tak dostaneš opět rovnoramenný trojúhelník - tentokrát ale s poloviční délkou stran - tj. 4 cm - obsah vypočteš tedy úplně stějně jako u toho velkého, jen se stranou 4cm (základna * výška to celé děleno 2 - výšku spočítáš pythagorovkou, jelikož víš 2 strany a úhel
Druhou možností je spočítat si obsah toho velkého a udělat si rovnici že V1=4*V2 a pak z toho vypočítat ten obsah
aha, tak ten tvůj dodatek trochu mění situaci - zkoukl jsem to a bral to jako rovnostranný
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.