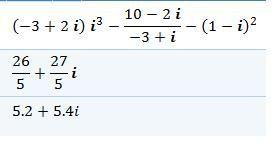Prosím o napsání postupu výpočtu této rovnice v komplexních číslech, pořád mi to nevychází.
(1 - 2i)x (a+bi) =2(a - bi) . i(2+i) mělo by to vyjít 7 +4i
a ještě jeden příklad: Vypočtěte v algebraickém tvaru (-3+2i)x i^3 - (10-2i)/-3+i + (-1-1)^2
1x
ASpoň zběžně ke druhému příkladu; dohodli jsme se tedy, že máme upravit výraz
(-3+2i)*i^3 - (10-2i)/(-3+i) + (-1-1)^2,
(respektive (-3+2i)*i³ - (10-2i)/(-3+i) + (-1-1)² ); zase místo x (krát) píšu hvězdičku.
co k tomu potřebujeme vědět:
za prvé, třetí mocnina i je -i (je to i krát druhá mocnina i, čili krát mínus jedna).
za druhé, komplexní číslo ze jmenovatele odstraníme tak, že zlomek rozžíříme komplexně sdruženým číslem ke jmenovateli, píšeme tedy
(10-2i)/(-3+i)¨= [(10-2i)/(-3+i)]*[(-3-i)/(-3-i)]= [(10-2i)*(-3-i)]/[(-3+i)*(-3-i)] = (-32-4i)/10 = (-16-2i)/5
další už je snadné, mělo by vyjít (pokud zadání jsem pochopil správně a nesekl jsem se ve výpočtech, což nemohu vyloučit) =(24+13i)/5
(-3 + 2i)⋅i3 = 2 + 3i
2 + 3i – (-16 – 2i)/5 + 4 = [10 + 15i – (-16 – 2i) + 20]/5 = (46 + 17i)/5
Nemohu než souhlasit,.
Vynechal jsem minus mzi prvními dvěma členy.
(tedy, pokud v zadání přeci jen nemá v té poslední závorce být místo -1-1 třžeba -1-i, ale když se tazatel dušuje, že ne...)
za první i druhý děkuji, ale ten druhý i přesto, že jste můj špatný zápis pochopili správně, ani jeden z výsledků nesouhlasí...
zkusil jsem to počítat znovu a tentokrát mi to vyšlo 10 - 5/2i a ani to neodpovídá...
0x
Než s tím začnu něco dělat, prosil bych o zkontrolování toho druhého zadání, tedy
(-3+2i)x i^3 - (10-2i)/-3+i + (-1-1)^2
Proč o tom píšu: jednak je mi divná ta poslední závorka (-1-1)^2 ; proč tem není rovnou -2? . A za druhé je mi podezřelý ten člen (ty členy) (10-2i)/-3+i ; nemá to čirou náhodou být (10-2i)/(-3+i)? Ono tak, jak je to napsáno, to smysl dává, ale raději se zeptám.
takhle je to tam prostě zadané 1-1... a to druhé je tam bez té závorky, ale to je přece stejné jako s tou závorkou...
V první příkladě: (a+bi)= z (a-bi)= z s pruhem
nerozepsané zadání je (1-2i)z = 2 z s pruhem - i(2+ i) a výsledek má tedy vyjít z=7+ 4i takto je to ve výsledcích.
Druhý příklad tam je to tedy takto 10-2i)/(-3+ i)
a výsledek má být ve tvaru a+ bi
2b - a -1) +(3b -2a+2)i = 0a vzniklý systém (2b - a -1) =0(3b -2a+2) = 0jistě bez problémů vyřešíte; řešení je tak, jak uvádíte.Příklad druhý byste měl umět, úpravy jsou podobné jako zde, ale když tak něco napíšu zvlášť.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.