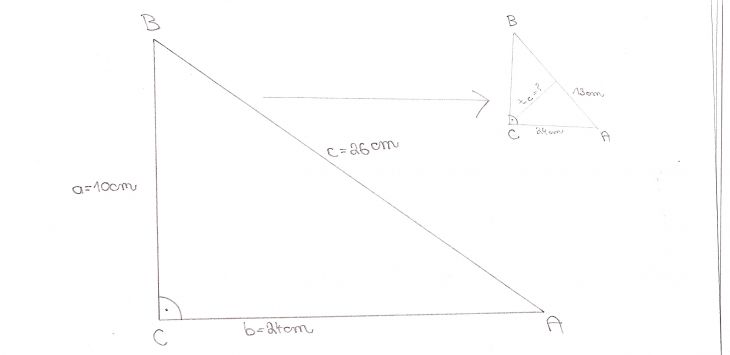
Dobrý den, ve sbírce úloh od Dr. Bělouna je na straně 59 tento příklad: Odvěsny pravoúhlého trojúhelníku ABC mají délky a = 10 cm, b = 24 cm. Vypočítejte délku těžnice tc.
Nevím, jak dojít k výsledku, pomocí Pythagorovy věty jsem si dopočítal stranu c, nyní však nevím, jak vypočítat těžnici. Pokud možno, taktéž Pyt. větou, nic složitého, jsem v 9. třídě. 
Přikládám obrázek:
2x
V tom trojúhelníku, který tam máte namalovaný, skutečně pravý úhel nebude (mimochodem, když to překreslujete do nového obrázku, ponechte písmena tak, aby odpovídala původnímu - nové C je úplně jiný bod než staré C, použijte raději třeba Sc), lze tam ale najít pravý úhel někde jinde.
Těžnice spojuje vrchol se středem protilehlé strany. Když vyznačíte středy všech stran a spojíte je spolu navzájem, vzniknou vám čtyři trojúhelníky, které jsou všechny podobné s tím původním, všechny mají pravý úhel. Dva z nich, kterými prochází hledaná těžnice, spolu vytvářejí obdélník, dal by se označit třeba C Sb Sc Sa. V něm jednu úhlopříčku vidíte, druhou úhlopříčkou je ta těžnice, jsou stejně dlouhé. Takže to vemete pythagorovou větou podle stran obdélníka (5 a 12), nebo prostě řeknete, že těžnice = úhlopříčka obdélníka = přepona malého trojúhelníku = polovina strany c.
doplněno 25.02.12 18:10:Joo, střední příčky se to jmenuje! :D Tlapka to tam má.
Děkuji moc, vyšlo mi to! Jen je velká škoda, že bych k tomu nikdy nedošel sám. Co si třeba počnu na písemce, to vskutku netuším. Nedokážu si to všechno takto představit. 
Proto je dobré procvičovat si všechny úkoly, co vám učitel zadá, nebo si najít i úlohy navíc v knížce. I když vám teď třeba poradíme, propočítáš si všechny možné typové úlohy. Vsadím se, že příště už to vědět budeš, když ses t ím teď setkal. 
Nic, co byste neprobrali, byste přece do písemky dostat neměli, a teď už víš, že nějaká možnost takovéhoto postupu tady je. 
Abych to upřesnil - pro výpočet pomocí pyt. věty mi chybí pravý úhel v nově vzniklém trojúhelníku.
Ahoj, já asi nepomohu Pythagorovou větou, ale wikipedia udává vzorec:
nebrali jste ho třeba ve škole, že bys ho mohl použít? Vychází to přes něj hezky.
Nevložil se... tady je celý odkaz: cs.wikipedia.org/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.