Vzpomněl jsem si, že jsme jako malí blbnuli s rukama a prstama a propíchanýma papírama, už nevím, jak jsme k tomu přišli, snad nám to fotr předváděl jako zajímavost. Šlo o to, že když se zakryje rukou oko a nechá se jen malinký průhled mezi prsty nebo v sevřené pěsti uvnitř zatočených prstů, je skrz něj vidět ostřeji. To samé s papírem, do kterého se propíchne díra špendlíkem.
Teď mi ale vrtá hlavou, jak že to funguje. O tomhle "pokusu"jsem nic nenašel, ale narazil jsem na nějaké povídání o dírkových foťácích a komorách, které mi vlastně nic neřeklo, jen potom v goo.gl/ruPqt na třetí stránce, pod Př.1: když se zvětší otvor, bude pronikat více světla, ale obraz na fotce se rozmaže. To mi smysl dává, i s tím názorným obrázkem. Každý elementární zdroj paprsku místo do jednoho bodu (s ideálně malou dírou) dopadne na větší plochu, takto se "rozprostřou"všechny elementární složky a výsledný obraz bude neostrý.
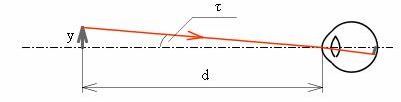
Oproti tomu v oku je ale spojná čočka. Paprsek v ose (z bodu, do kterého se oko dívá, 0°) projde rovně na sítnici. Ten bude zaostřený pokaždé, že? Kdyby byl z libovolně vzdáleného bodu vyslán směrový nerozbíhavý paprsek (laser) s minimální šířkou (aby nedopadl na plochu 3x3mm, ale prostě přesně do jednoho místa), byl by vidět ostře, bez ohledu na přiblížení a oddálení zdroje.
Problém nastane, když je zdroj všesměrový (žárovka) nebo je zdrojem předmět (v odraženém, denním světle), protože kromě toho paprsku v úhlu 0° do zornice oka dorazí i paprsky pod úhlem +1°, +2°, -1°, -2°atd, a pak už záleží na vytvarování čočky a zaostření oka, aby je spojka "ohnula"zpět k ose a ony se protly s osou přesně na sítnici. Když do roviny osy dorazí už před nebo až za sítnicí, jeden zdrojový bod se tak promítne ne do bodu, ale na plochu, a oko uvidí rozmazaně. (Tenhle odlišný úhel bude platit u blízkých předmětů; u vzdálených to budou rovnoběžné paprsky na celou plochu zornice, které se neohnou všechny do ohniska, ale pouze do přibližného okolí.)
Když se podívám na stickynote papírek popsaný lihovkou, 8x8cm, písmena tak 2cm, ze dvou metrů za dobrého světla, holým okem uvidím akorát tak oranžový flek. Když vemu kus tvrdšího papíru, udělám nůžkama 1.5mm dirku, podržím 1-2cm před okem, uvidím ho (víceméně, dostatečně na přečtení) ostře. Je to proto, že paprsky místo dopadu na celou plochu zornice o průměru nějakých 6mm, kterých by bylo mnoho a které by se za čočkou špatně lomily a dopadly na velké místo naprosto rozmazané, teď procházejí jen 1.5mm otvorem, sice se rozmažou taky, ale zdaleka ne tolik, zůstanou ostřejší?
Takže k otázce(otázkám) - vysvětluju si to správně? ![]() Kdyby šla udělat ještě menší dírka, fungovalo by to stejně pro pohled nablízko při dalekozrakosti?
Kdyby šla udělat ještě menší dírka, fungovalo by to stejně pro pohled nablízko při dalekozrakosti?
Když se tímto papírkem trochu pohne, zdánlivě se hýbe i cílový objekt, je to proto, že místo průchodu svazku paprsků kolem 0° (v ose pohledu) projde svazek trochu vedle (ale samozřejmě pořád skrz zornici), tedy po zlomu v čočce dorazí na sítnici ze šikmého směru?
0x
Tyto paprsky se neohnou a neprotnou se na sítnici s osou _ viz obrázek.
Zde je něco málo o vlivu velikosti dírky na obraz a proč se používají čočky: http://cmp.felk.cvut.cz/ drbohlav/TeachPres/03GeomOpticsCz.pdf
doplněno 19.02.12 17:24:
Při vložení odkazu mi to odstranilo tyldu před jménem drbohlav. http://1url.cz/2zZB
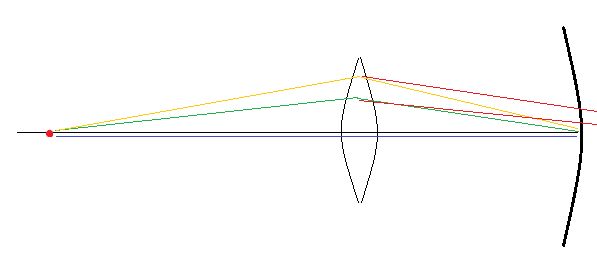
Asi abych to lépe vysvětlil: Zdrojem nebude předmět, ale jen jeden bod. Čočka v oku má nějaký vlastní rozměr, proto na její plochu dopadají paprsky pod různými úhly. Modrý projde přímo a trefí správné místo na sítnici pokaždé. Zelený a oranžový se ale bude lámat podle zakřivení čočky, s nedostatečným zakřivením podle červených čar, takže se jeden bod v předmětovém prostoru nepromítne jako jeden bod v obrazovém prostoru na sítnici, ale jako rozmázlý flek.
Když se tento rozptyl paprsků nahoru a dolů od osy zmenší (třeba tou dírou v papíru), oranžový neprojde, vejde se do ní jen ten zelený, bude rozmáznutý flek také menší, tedy ostřejší. Jde mi pouze o to, jestli si toto vysvětluju správně?
V odkazovaném pdf to je vlastně porovnání na straně 7. Případ c, optimum - je zaostření při zmenšení dírky způsobeno tím, co popisuju? (před tím, než se to zvrtne do možnosti b, kdy už dochází k ohybu)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.